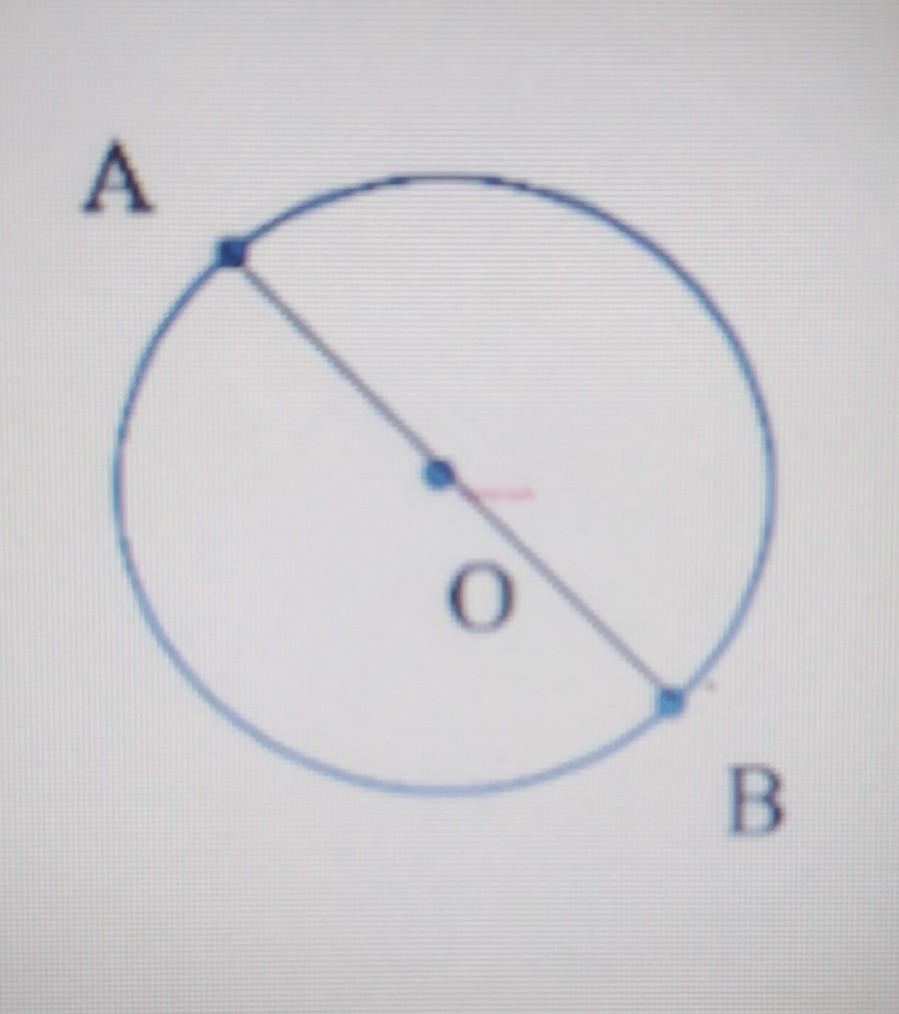
Известно, что AB - диаметр окружности. А (2; 4), В(8; -4).
A) Найти координаты точки О - центра окружности (по формуле
середины отрезка)
B) Bчислить радиус окружности r (по формуле расстояния между
точками)
С) Записать уравнение этой окружности (использовать общую формулу окружности).
Приложения:
Ответы на вопрос
Ответил orjabinina
0
Объяснение:
А) х=(х₁+х₂):2 ,у=(у₁+у₂):2 ,где (х₁;у₁), (х₂;у ₂) -координаты концов отрезка , (х;у)-координаты середины.
А(2;4) ,В(8;-4) . О-середина АВ , найдем ее координаты.
х(О)= ( х(А)+х(В) )/2 у(О)= ( у(А)+у(В) )/2
х(О)= ( 2+8 )/2 у(О)= ( 4-4 )/2
х(О)= 5 у(О)= 0
О( 5 ; 0) .
В) d=√( (х₁-х₂)²+(у₁-у₂)² ), где (х₁;у₁), (х₂;у ₂) -координаты концов отрезка.
АО=√( (5-2)²+(0-4)² )=√(9+16)=5.
С) Уравнение окружности (x – х₀)²+ (y – у₀)² = R² , (х₀ ; у₀)-координаты центра.
(x – 5)²+ (y – 0)² = 5²
(x – 5)²+ y² =25
Ответил ant20202020
0
а)х₀=(2+8)/2=5
у₀=(4-4)/2=0
А(2;4); О(5;0)
в) АО=√((5-2)²+(0-4)²)=√(25)=5
с) общая формула (х-х₀)²+(у-у₀)²=R²
(х-5)²+(у-0)²=5²
или так (х-5)²+у²=5²
Новые вопросы