изобразите на координатной плоскости множество решений неравенства

​

Ответ:

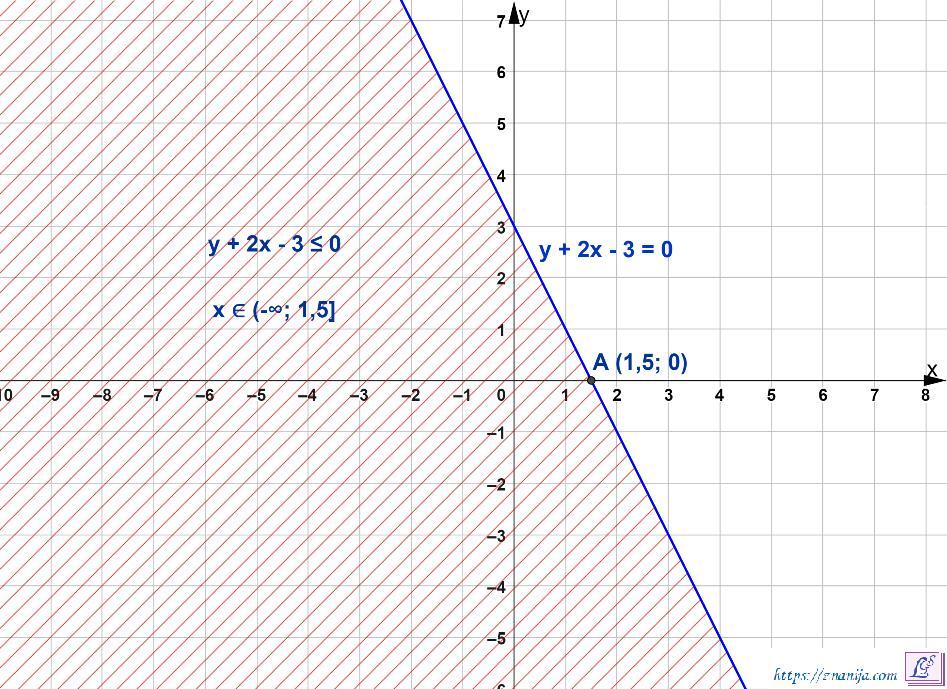
Решением неравенства y + 2x - 3 ≤ 0 являются все точки координатной плоскости, абсцисса которых x ∈ (-∞; 1,5], а ордината  удовлетворяет условию: y ≤ -2x + 3

Объяснение:

Рисунок прилагается.

y + 2x - 3 ≤ 0

Преобразуем неравенство: y ≤ -2x + 3

Условию неравенства удовлетворяют все точки плоскости, которые находятся ниже графика линейной функции y = -2x + 3, включая и точки самого графика, так как неравенство не строгое.

Построим график линейной функции y = -2x + 3 (он же y +2x - 3 = 0). Для его построения достаточно рассчитать две точки.

При x = 0 y = 3 (точка (0; 3));

при x = 1,5 y = 0 (точка (1,5; 0))

Решением неравенства будут все точки плоскости, абсцисса которых

x ∈ (-∞; 1,5], а ордината  удовлетворяет условию: y ≤ -2x + 3