Алгебра, вопрос задал charliemoon113 , 2 года назад

Избавьтесь от иррациональности в знаменателе дроби:

Приложения:

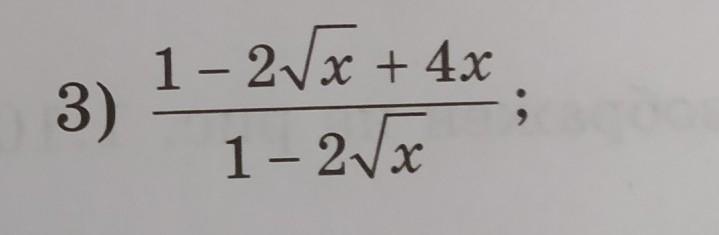
Ответы на вопрос

Ответил ldglkva

1

Ответ:

$\displaystyle \frac{1-2\sqrt{x}+4x }{1-2\sqrt{x} } = \frac{1-8x\sqrt{x} }{1-4x}$

Объяснение:

$\displaystyle \frac{1-2\sqrt{x}+4x }{1-2\sqrt{x} } = \frac{(1-2\sqrt{x}+4x)(1+2\sqrt{x}) }{(1-2\sqrt{x})(1+2\sqrt{x}) } = \frac{((1-2\sqrt{x})+4x)(1+2\sqrt{x}) }{1-4x} =\\\\\\\frac{(1-2\sqrt{x})(1+2\sqrt{x})+4x(1+2\sqrt{x}) }{1-4x} =\frac{1-4x+4x+8x\sqrt{x} }{1-4x} =\\\\ = \frac{1-8x\sqrt{x} }{1-4x}$

Использована формула разности квадратов:

a² - b² = (a - b)(a + b)

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Английский язык, 1 год назад

Напишите пожалуйста рассказ на ангийском языке "каким я буду через 10 лет" меня зовут марсель и мне 12 лет...

Информатика, 1 год назад

помогите пожалуйста по информатике прошу вас...

Английский язык, 2 года назад

Преобразуйте предложения в прошедшее время. It’s a pity to find him ill. (Жаль найти его больным.) Помогите пожалуйста срочно надо! Даю 14 балов It seems to me that Anna is 17. (Мне кажется, что...

Алгебра, 2 года назад

Срочно!!! Алгебра 8 класс, лёгкие примеры, просто мы тупые...

География, 7 лет назад

Основными импортерами железной руды являются:а) западная Европа б) западная Европа и Японияв) США и западная Европа...

Математика, 7 лет назад

При каком значении x будет верно равенство : а)12/x=3/4 б)1/5=x/45 в)60/100=x/5 г)5/100=3/x д)x/5=20/100 е)13/65=x/5 Пожалуйста можно подробнее, чтобы понять задание, спасибо заранее.