Из вершины В треугольника АВС, сторона АС которого лежит в плоскости а(альфа), проведен к этой плоскости перпендикуляр ВВ1. Найдите расстояние от тгчки В до прямой АС и до плоскости а(альфа), если АВ=2см, уголВАС=150° и двугранный угол ВАСВ1 равкн 45°.

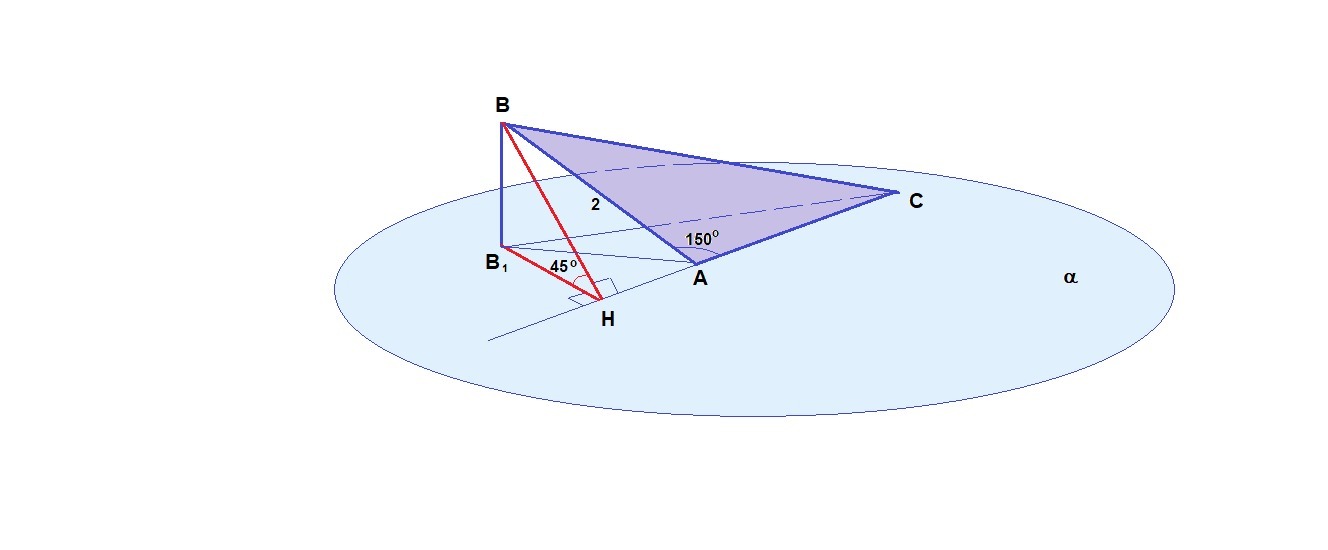
В плоскости α проведем В₁Н⊥АС. В₁Н - проекция ВН на плоскость α, значит ВН⊥АС по теореме о трех перпендикулярах. Значит

        ∠ВНВ₁ = 45° - линейный угол двугранного угла ВАСВ₁;

        ВН - высота треугольника АВС, искомое расстояние от точки В до прямой АС.

∠ВАН = 180° - ∠ВАС = 180° - 150° = 30° по свойству смежных углов.

В прямоугольном треугольнике АВН, ВН = 1/2 АВ = 1 см по свойству катета, лежащего напротив угла в 30°.

Итак, расстояние от точки В до прямой АС

         ВН = 1 см.

ВВ₁ - расстояние от точки В до плоскости α.

ΔВВ₁Н: ∠ВВ₁Н = 90°

            ВВ₁ = ВН · sin45° = 1 · √2/2 = √2/2 см