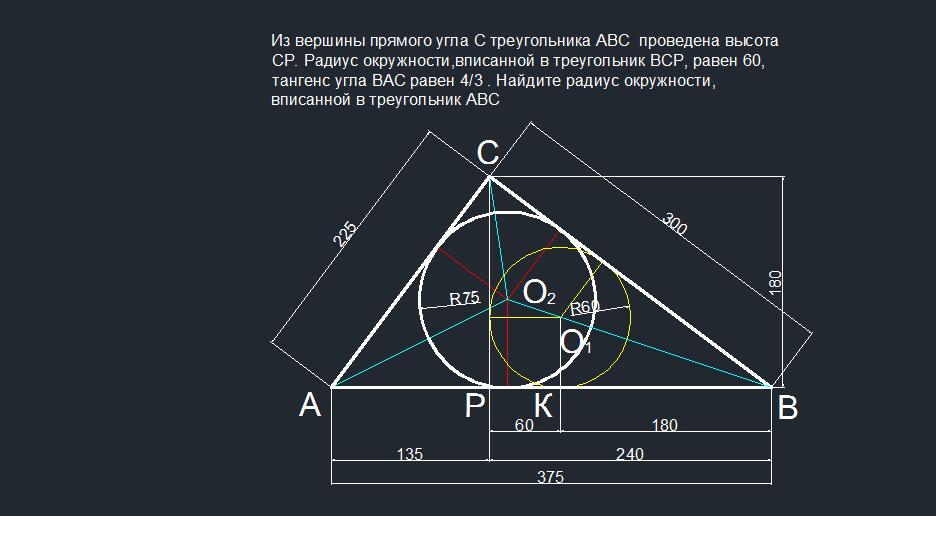
Из вершины прямого угла С треугольника ABC проведена высота CP .Радиус окружности,вписанной в треугольник BCP ,равен 60 ,тангенс угла BAC равен 4/3 . Найдите радиус окружности ,вписанной в треугольник ABC .
ребят пожалуйста по быстренькому
Ответы на вопрос
Ответил dnepr1
0
Так как центр вписанной окружности находится на биссектрисе угла, то надо найти тангенс половины угла АВС.
tg ABC = tg(90-CAB) = ctg CAB = 1 / (4/3) = 3/4.
Тангенс половинного угла АВС обозначим х. Найдем его через тангенс угла АВС. 3/4 = 2х / (1 - х²). 3х²+8х-3=0 Д = 8²+4*3*3=100
х₁ = (-8+10) / 6 = 1/3 х₂ = (-8-10) / 6 = -3 (не принимается отрицательное значение ). Отсюда значение отрезка ВК = 60/(1/3) = 180, а ВР = 180+60 = 240. Высоту СР находим через тангенс угла АВС:
ВР = 240*(3/4) = 180. Отрезок АР = 180 / (4/3) = 135. Сторона АС = 135 + 240 = 375. Сторона АС = √(135²+180²) = 225, СВ = √(180²+240²= 300, Площадь треугольника АВС = (1/2)*375*180=33750.
Полупериметр равен (225+300+375) / 2 = 450.
Радиус окружности ,вписанной в треугольник ABC равен:
r = S / p = 33750 / 450 = 75.
tg ABC = tg(90-CAB) = ctg CAB = 1 / (4/3) = 3/4.
Тангенс половинного угла АВС обозначим х. Найдем его через тангенс угла АВС. 3/4 = 2х / (1 - х²). 3х²+8х-3=0 Д = 8²+4*3*3=100
х₁ = (-8+10) / 6 = 1/3 х₂ = (-8-10) / 6 = -3 (не принимается отрицательное значение ). Отсюда значение отрезка ВК = 60/(1/3) = 180, а ВР = 180+60 = 240. Высоту СР находим через тангенс угла АВС:
ВР = 240*(3/4) = 180. Отрезок АР = 180 / (4/3) = 135. Сторона АС = 135 + 240 = 375. Сторона АС = √(135²+180²) = 225, СВ = √(180²+240²= 300, Площадь треугольника АВС = (1/2)*375*180=33750.
Полупериметр равен (225+300+375) / 2 = 450.
Радиус окружности ,вписанной в треугольник ABC равен:
r = S / p = 33750 / 450 = 75.
Приложения:
Новые вопросы
Українська мова,
2 года назад
Английский язык,
2 года назад
Математика,
9 лет назад
Биология,
9 лет назад