Из вершины прямого угла прямоугольного треугольника проведена медиана, которая является так же биссектрисой. Докажите, что медиана делит этот треугольник на два равных треугольника.
Ответы на вопрос
Ответил nafanya2014
0
Медиана, проведенная из вершины прямого угла треугольника равна половине гипотенузы.
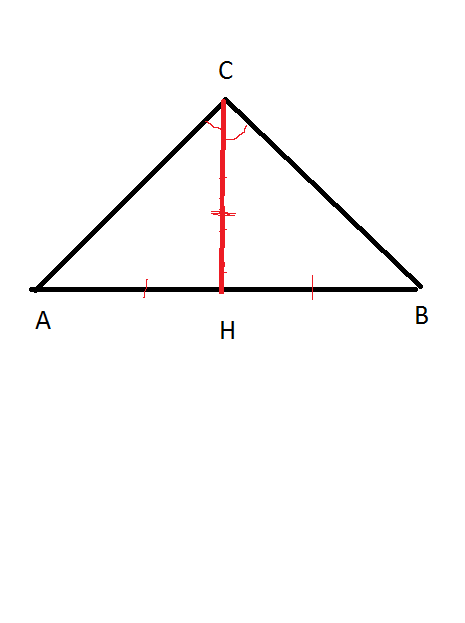
СН=АН=ВН
Так как медиана является и биссектрисой, то ∠АСН=∠ВСН=45°
Треугольник АСН - равнобедренный, так как СН=АН, а значит
∠САН=∠АСН=45°, а ∠АНС=180°-45°-45°=90°.
Треугольник АСН - прямоугольный, равнобедренный
Треугольник ВСН - равнобедренный, так как СН=ВН, а значит
∠СВН=∠ВСН=45°, а ∠ВНС=180°-45°-45°=90°
Прямоугольные треугольники АСН и ВСН равны по катету (СН-общий) и острому углу ∠АСН=∠ВСН=45°
СН=АН=ВН
Так как медиана является и биссектрисой, то ∠АСН=∠ВСН=45°
Треугольник АСН - равнобедренный, так как СН=АН, а значит
∠САН=∠АСН=45°, а ∠АНС=180°-45°-45°=90°.
Треугольник АСН - прямоугольный, равнобедренный
Треугольник ВСН - равнобедренный, так как СН=ВН, а значит
∠СВН=∠ВСН=45°, а ∠ВНС=180°-45°-45°=90°
Прямоугольные треугольники АСН и ВСН равны по катету (СН-общий) и острому углу ∠АСН=∠ВСН=45°
Приложения:
Ответил Аноним
0
Рисунок можно? Я не понимаю где эти ваши ch ah bh
Ответил nafanya2014
0
Рисунок есть
Новые вопросы