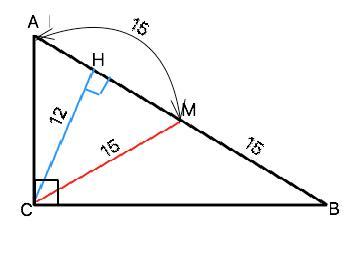
Из вершины прямого угла прямоугольного треугольника проведены его высоты и медиана, равные соответственно 12 см и 15 см. Найдите стороны и синусы острых углов этого трегольника
Ответы на вопрос
Ответил Hrisula
0
Ответ: катеты 6√5 см и 12√5 см, гипотенуза 30 см. Синусы острых углов 1/√5 и 2/√5
Объяснение: Сделаем согласно условию рисунок и обозначим вершины треугольника АВС ( угол С=90°).
СН=12 см - высота. СМ - медиана. По свойству медианы прямоугольного треугольника из прямого угла АМ=ВМ=СМ=15 см. =>
АВ=2•15=30 см
Из прямоугольного ∆ СНМ катет НМ равен 9 ( египетский). Тогда АН=АМ-МН=15-9=6 ⇒
из ∆ АНС по т. Пифагора АС= √(CH²+AH²)=√180=6√5
из ∆ ВНС по т. Пифагора ВС=√(CН²+BH²)=√720=12√5
Синус угла равен отношению противолежащего ему катета к гипотенузе.
sin ∠CAB=AC:AB=(6√5):30=1/√5 или ≈0,4472
sin ∠CBA=BC:AB=(12√5):30=2/√5 или ≈0,8944
Приложения:
Новые вопросы
Математика,
1 год назад
Алгебра,
1 год назад
Математика,
7 лет назад
Экономика,
7 лет назад
Химия,
8 лет назад