Из точки P, удаленной от плоскости a 4√3 см, к этой плоскости проведена наклонная, образующая угол 60° с плоскостью a. Найдите длину этой наклонной.
помогите, пожалуйста
Ответы на вопрос
Ответил mathkot
0
Ответ:
8 см
Объяснение:
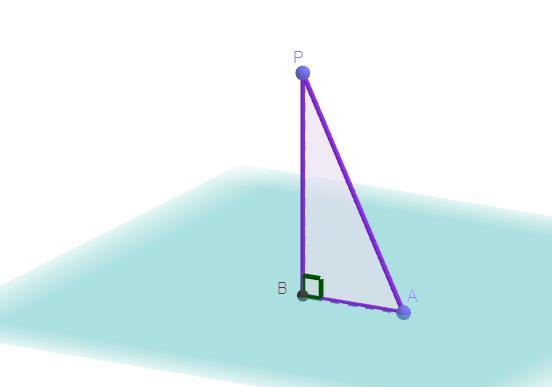
Дано: BP = см, ∠PAB = 60°, BP ⊥ AB
Найти: AP - ?
Решение: Рассмотрим прямоугольный треугольник ΔBAP:
см.
Приложения:
Новые вопросы