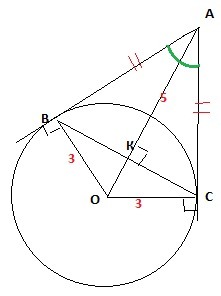
Из точки А к окружности радиуса 3 см проведены две касательеык АВ и АС. Найдите длину отрезка ВС если расстояние от токэчки А до центра окружности равно 5 см.
Ответы на вопрос
Ответил товик
0
Из свойства касательных:
1. касательная к окружности перпендикулярна к радиусу, проведенному в точку касания⇒
∠ОСА=90°, тогда по т. Пифагора АС=√(ОА²-ОС²)=√(25-9)=4см;
2. отрезки касательных к окружности, проведенных из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности⇒
АС=АВ, ΔАВС-равнобедренный, в равнобедренном Δ биссектриса является высотой и медианой. АК⊥ВС, ВК=КС.
Используем соотношение пропорциональных отрезков:
в прямоугольном треугольнике каждый катет есть среднее пропорциональное между гипотенузой и проекцией катета на гипотенузу, поэтому в ΔОВА АК=АВ²/ОА=16/5=3,2см,
ОК=ОА-АК=5-3,2=1,8 см.
ΔОВК-прямоугольный, ВК=√(ОВ²-ОК²)=√(9-3,24)=2,4см
ВС=2ВК=2*2,4=4,8см
1. касательная к окружности перпендикулярна к радиусу, проведенному в точку касания⇒
∠ОСА=90°, тогда по т. Пифагора АС=√(ОА²-ОС²)=√(25-9)=4см;
2. отрезки касательных к окружности, проведенных из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности⇒
АС=АВ, ΔАВС-равнобедренный, в равнобедренном Δ биссектриса является высотой и медианой. АК⊥ВС, ВК=КС.
Используем соотношение пропорциональных отрезков:
в прямоугольном треугольнике каждый катет есть среднее пропорциональное между гипотенузой и проекцией катета на гипотенузу, поэтому в ΔОВА АК=АВ²/ОА=16/5=3,2см,
ОК=ОА-АК=5-3,2=1,8 см.
ΔОВК-прямоугольный, ВК=√(ОВ²-ОК²)=√(9-3,24)=2,4см
ВС=2ВК=2*2,4=4,8см
Приложения:
Новые вопросы