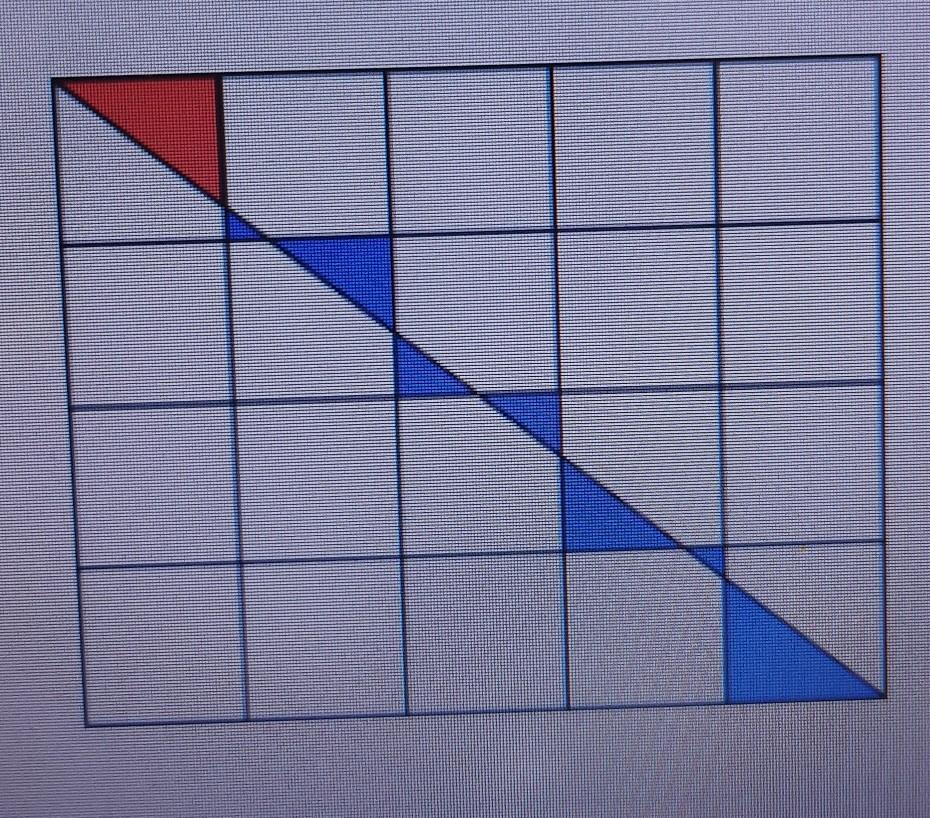
Из 20 одинаковых квадратов сложили прямоугольник 4 x 5. Из левого верхнего угла прямоугольника в его правый нижний угол проведена диагональ. Она отсекает треугольники от некоторых квадратов. Периметр красного треугольника равен 1. Найдите суммарный периметр синих треугольников.
Ответы на вопрос
Ответ: 4
Пошаговое объяснение:
Чтобы найти сумму периметров всех цветных прямоугольных треугольников (синих и красного), необходимо сложить длины всех их сторон, иначе говоря, нужно сложить длины всех вертикальных и горизонтальных катетов, а также и все их гипотенузы.
При сложении длин всех вертикальных катетов, получаем ширину прямоугольника, при сложении длин всех горизонтальных катетов получаем длину прямоугольника, наконец, при сложении всех гипотенуз мы получаем диагональ прямоугольника.
То есть сумма периметров цветных треугольников равна периметру большего прямоугольного треугольника, катеты которого являются длиной и шириной прямоугольника, а гипотенуза которого является диагональю прямоугольника.
Очевидно, что красный треугольник подобен большему прямоугольному треугольнику по острому углу между гипотенузой и горизонтальным катетом.
По условию наш прямоугольник разбит на 4x5 квадратов.
Иначе говоря, длина прямоугольника (она же горизонтальный катет большего треугольника) по длине равна 5 сторонам квадрата, при этом длина горизонтального катета красного треугольника равна 1 стороне квадрата, а значит периметр большего прямоугольного треугольника в 5 раз больше периметра красного, то есть равен 1*5=5.
Таким образом, сумма периметров цветных треугольников равна 5, а значит суммарный периметр синих треугольников равен 5 - 1 = 4.
Відповідь:
Суммарный периметр синих треугольников равен 4 единицам.
Покрокове пояснення:
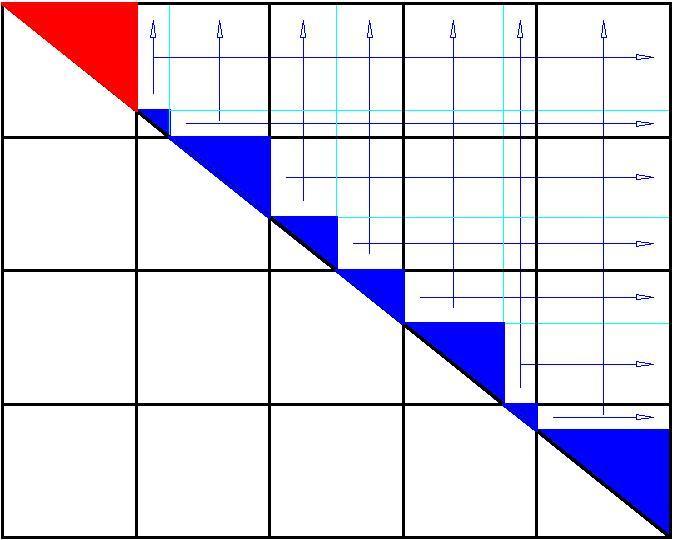
Для удобства заменим треугольники находящиеся ниже диагонали на аналогичные, размещенные выше диагонали ( смотри рисунок ).
Если разбить треугольник на три составляющих его отрезка и сдвинуть горизонтальные участки вверх до внешних границ большого прямоугольника, я вертикальные - в лево. Видно, что суммарная величина всех горизонтальных участков равна длине прямоугольника ( 5 квадратам), а суммарная величина всех вертикальных участков равна ширине прямоугольника ( 4 квадратам ). Суммарная величина всех наклонных участков равна диагонали прямоугольника.
Большой треугольник, образованный диагональю и внешними границами прямоугольника подобен красному треугольнику ( по трем углам ). Коэффициент подобия равен 5, так как все стороны красного треугольника в 5 раз меньше большого треугольника. Следовательно периметр большого треугольника и как следствие суммарный периметр одного красного и восьми синих треугольников равен 1 × 5 = 5 единицам.
Суммарный периметр синих треугольников равен 5 - 1 = 4 единицы ( мы вычли из суммарного периметра всех 9 треугольников периметр красного треугольника ).