Исследуйте функцию и постройте график у=6х⁵+15х⁴+10х³ .Помоги пожалуйста .

 y=6x⁵+15x⁴+10x³

1)  Область определения: х∈(-∞,+∞) .

2)  Множество значений: у∈(-∞,+∞) .

3)  Эта кривая не имеет асимптот, так как

.

Нет точек разрыва.

4)  Точка пересечения с осью ОУ (при х=0) одна - это (0,0).

5)  Точка пересечения с осью ОХ тоже одна - (0,0) , так как

6)  Интервалы монотонности и точки экстремума функции:

Подсчитаем знаки производной  y'  на полученных интервалах:

При переходе через точки х=0 и х= -1 производная не меняет знак, значит точки х=0 и х= -1 не являются точками экстремума. А на промежутках, где производная всюду положительна, сама функция возрастает.

Интервалы возрастания функции:  x∈(-∞,-1 ]∪[-1,0 ]∪[0,+∞) .

7) Интервалы выпуклости и вогнутости, точки перегиба функции:

Определим знаки второй производной y'' на интервалах:

На промежутках, где y''<0, функция y(x) выпукла, а там, где y''>0, функция вогнута. Точки перегиба - те точки, при переходе через которые у'' меняет знак,это х= -1 , х= -0,5 , х=0 .

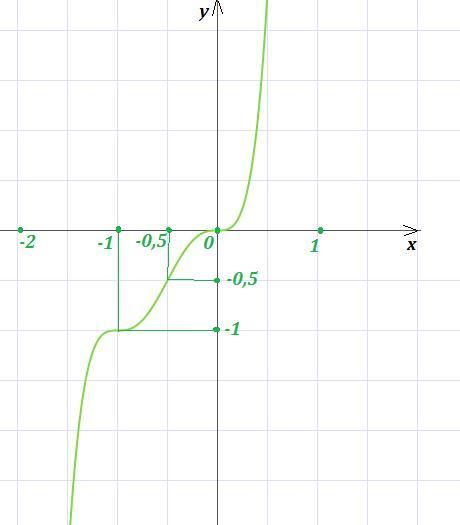
8)  Для более точного построения графика найдём координаты некоторых промежуточных точек:  (-1,-1)  ,  (-0,5 ; -0,5) .

График на рисунке.