Алгебра, вопрос задал Xonda7777 , 1 год назад

Исследовать абсолютную и условную сходимость рядов.

Приложения:

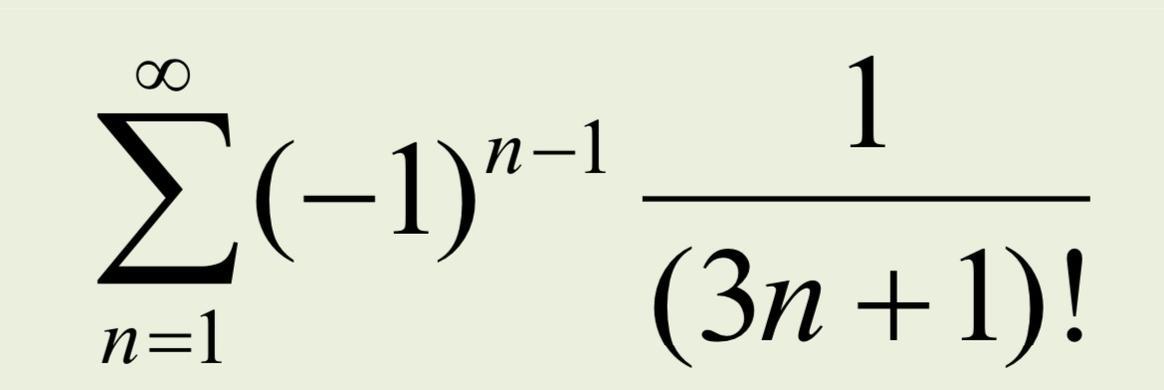
Ответы на вопрос

Ответил Alnadya

2

Решение.

$\bf \sum \limits _{n=1}^{\infty }(-1)^{n-1}\dfrac{1}{(3n+1)!}$

Проверим выполнение условий признака Лейбница сходимости знакопеременных рядов .

$\bf 1)\ \ |a_1| > |a_2| > |a_3| > \ ...\\\\|a_{n}|=\dfrac{1}{(3n+1)!}\ \ ,\ \ \ \ \ \dfrac{1}{4!} > \dfrac{1}{7!} > \dfrac{1}{10!} > ...\\\\\\2)\ \ \lim\limits_{n \to \infty}|a_{n}|= \lim\limits_{n \to \infty}\dfrac{1}{(3n+1)!}=\Big[\dfrac{1}{\infty }\Big]=0$

Условия признака Лейбница выполнены . Ряд сходится по признаку Лейбница .

Проверим на абсолютную сходимость . Применим признак Даламбера к ряду, составленному из абсолютных величин , то есть к ряду $\bf \sum \limits _{n=1}^{\infty }\dfrac{1}{(3n+1)!}$ .

$\bf \displaystyle \lim\limits_{n \to \infty}\, \frac{|a_{n+1}|}{|a_{n}|}= \lim\limits_{n \to \infty}\, \frac{1}{(3n+4)!}:\frac{1}{(3n+1)!}=\lim\limits_{n \to \infty}\, \frac{(3n+1)!}{(3n+4)!}=\\\\\\=\lim\limits_{n \to \infty}\frac{1}{(3n+2)(3n+3)(3n+4)}=0 < 1$

Ряд, составленный из абсолютных величин, сходится .

Исходный знакочередующийся ряд сходится абсолютно .

Приложения:

Xonda7777: Спасибо вам огромное

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Окружающий мир, 11 месяцев назад

Визначити час і дату: а) в Сіднеї; б) в Лондоні; в) у Нью-Йорку, якщо місцевий час у м. Торецьк (37° 52' сх. д.) 1 год 30 хв, а дата - 12 березня.

Экономика, 11 месяцев назад

Розрахувати податок на нерухомість за 2020 та 2021 р. для сім’ї, що складається з п’яти осіб: чоловік (резидент Італії), дружина (резидент України) і троє неповнолітніх дітей. Дружина володіє 2...

Математика, 1 год назад

Два лыжника стартовали с интервалом 2 мин. На каком расстоянии от старта они встретятся, если второй лыжник бежит со скоростью 20 км/ч, а первый - 18 км/ч?

Литература, 1 год назад

Записи про Шерлока Холмса ВСЕ ПЕРСОНАЖИ -И КТО ОНИ Пример:Сильвія - мати Елі И так о каждом пожалуйста!!! Нужно сегодня!!

Математика, 6 лет назад

Сколько квадратов изображено на картинках? Создайте аналогичную задачу самостоятельно...

Биология, 6 лет назад

выбери правельный ответ. Источники энергии в зависимости от их преобразования и способов получение энергии делятся на какие?