Алгебра, вопрос задал adskiymatematik , 6 лет назад

интегрирование по частям помогите нужно решение ответ есть

Приложения:

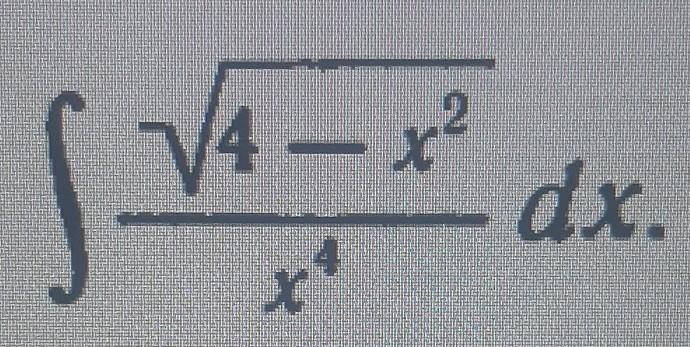
NNNLLL54: здесь проще не по частям интегрировать, а заменой

Ответы на вопрос

Ответил NNNLLL54

1

Ответ:

Вычисляем интеграл с помощью тригонометрической подстановки.

$\displaystyle \int \frac{\sqrt{4-x^2}}{x^4}\, dx=\Big[\ x=2sint\ ,\ dx=2cost\, dt\ ,\ 4-x^2=4-4sin^2t=\\\\\\=4(1-sin^2t)=4cos^2t\ \Big]=\int \frac{\sqrt{4cos^2t}}{2^4sin^4t}\cdot 2cost\, dt=\int \frac{4cos^2t}{2^4sin^4t}\, dt=\\\\\\=\frac{1}{4} \int ctg^2t\cdot \frac{dt}{sin^2t}=-\frac{1}{4}\int ctg^2t\cdot d(ctgt)=-\frac{1}{4}\cdot \frac{ctg^3t}{3}+C=\\\\\\=-\frac{1}{12}\cdot ctg^3(arcsin\frac{x}{2})+C=-\frac{1}{12}\cdot \Big(\frac{\sqrt{4-x^2}}{x}\Big)^3+C=-\frac{\sqrt{(4-x^2)^3}}{12\, x^3}+C$

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Русский язык, 1 год назад

СРОЧНО Придумать слова с чередованием к слову приближался,входят,выезжают,звук,перетащить,ремень,сижу,берег,кажется,плещут,овраг,просить,городок,узел,купец,золото.И УКАЗАТЬ ГДЕ ТАМ ЧЕРЕДОВАНИЕ ДАЮ 40...

Русский язык, 1 год назад

выпиши слова на орфорграмму непроверяемые главные в корне слова. конечно, кирпичный , наверняка, симпатичный, щенка, никто, никогда. помогите пожалуйста :-( прошу вас. заранее спасибо.

Алгебра, 6 лет назад

Срочно!!!!!!!!!!!!!!

Алгебра, 6 лет назад

(8 + x)8- ax) +(x+ 2) $68 + 4x$ ...

Информатика, 8 лет назад

Дан массив, состоящий из целых чисел. Нумерация элементов начинается с 0. Напишите программу, которая выведет элементы массива, номера которых четны (0, 2, 4...).

Алгебра, 8 лет назад

Пожалуйста, решите кто нибудь. Очень надо.