Математика, вопрос задал repvbx1999 , 7 лет назад

Интегралы
Пожалуйста напишите помимо решения примененную формулу или способ

Приложения:

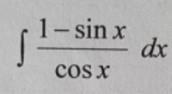
Ответы на вопрос

Ответил aastap7775

$sin2x = frac{2tanx}{1+tan^2x}\cos2x = frac{1-tan^2x}{1+tan^2x}\int frac{1-sinx}{cosx}dx = int frac{1 - frac{2tanfrac{x}{2}}{1+tan^2frac{x}{2}}}{frac{1-tan^2frac{x}{2}}{1+tan^2frac{x}{2}}}dx = int frac{1+tan^2frac{x}{2}-2tanfrac{x}{2}}{1-tan^2frac{x}{2}}dx = int frac{(tanfrac{x}{2}-1)^2}{(1-tanfrac{x}{2})(1+tanfrac{x}{2})}dx = int frac{1-tanfrac{x}{2}}{1+tanxfrac{x}{2}}dx = |tanfrac{x}{2} = t => frac{x}{2} = atant => x = 2atant = dx = frac{2}{1+t^2}dt| =$

$= int frac{1-t}{(1+t)(1+t^2)}*2dt = int frac{2-2t}{(t^2+1)(t+1)}dt = | frac{2-2t}{(t^2+1)(t+1)} = frac{At+B}{t^2+1} + frac{C}{t+1} = frac{At^2 + Bt + At + B + Ct^2 + C}{(t^2+1)(t+1)} = frac{t^2(A+C) + t(A+B) + C}{(t^2+1)(t+1)} => C = 2, A = -2, B = 0| = int (frac{2}{t+1} - frac{2t}{t^2+1})dt = 2ln|t+1| - ln(t^2+1) + c = 2ln|tanfrac{x}{2}+1| - ln(tan^2frac{x}{2}+1)+c = 2ln|tanfrac{x}{2}+1| - ln(frac{1}{cos^2frac{x}{2}})+c = 2ln|tanfrac{x}{2}+1| + 2ln|cosfrac{x}{2}| + c =$ $=2(ln|tanfrac{x}{2}+1| + ln|cosfrac{x}{2}|) + c = 2ln|(tanfrac{x}{2}+1)cosfrac{x}{2}| + c = 2ln|sinfrac{x}{2}+cosfrac{x}{2}| + c = ln(sinfrac{x}{2}+cosfrac{x}{2})^2 + c = ln(1+sinx)+lnC = ln(C+Csinx)$