интеграл пи на 12 dx sin2(x+пи/6) dx.
Приложения:
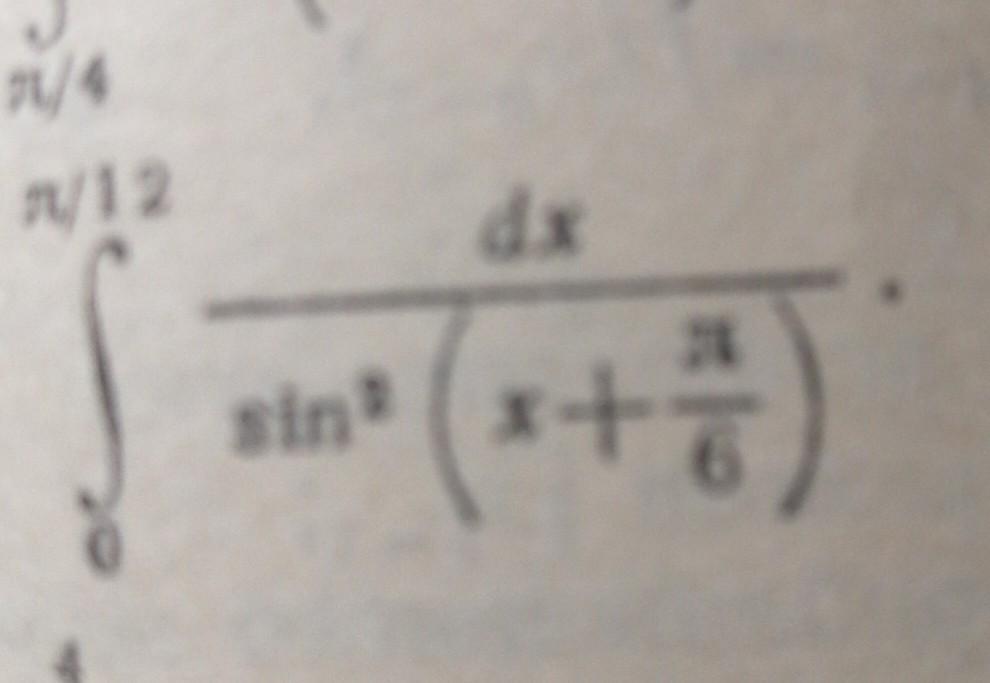
Ответы на вопрос
Ответил Lixu
1
Ответ:
(√3)-1
Решение
Сначала мы можем загнать (x+π/6) под знак дифференциала , т. е. dx=d(x+π/6)
Так как d(x+π/6)=dx нечего в интеграле не поменяется , но теперь мы будем интегрировать по переменой x+π/6
x+π/6 мы мысленно можем заменить на t
Тогда получим интеграл от функции dt/sin²t
такой интеграл равен -1/tg(t)
Теперь делаем обратную замену , получаем -1/tg(x+π/6)
tg-тангенс , (если что) .
Потом просто нужно подставить пределы интегрирования , и после сокращения будет (√3)-1
Более подробное решение находится на фотографии выше ↑
Удачи в следующих вычислениях
Приложения:

Новые вопросы
Русский язык,
1 год назад
Русский язык,
1 год назад
Физика,
2 года назад
Математика,
2 года назад
Математика,
7 лет назад
Биология,
7 лет назад