Математика, вопрос задал Mi9478 , 1 год назад

Интеграл дробно-рациональной функции.

Приложения:

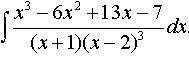
Ответы на вопрос

Ответил sebrithien

$∫ \frac{1}{x + 1} + \frac{1}{ {(x - 2)}^{3} } dx \\ ∫ \frac{1}{x + 1} dx + ∫ \frac{1}{ {(x - 2)}^{3} } dx \\ In( |x + 1| ) - \frac{1}{2 {(x - 2)}^{2} } \\ In( |x + 1| ) - \frac{1}{2 {(x - 2)}^{2} } + C , \: C∈R$

Ответил NNNLLL54

$\int \frac{x^3-6x^2+13x-7}{(x+1)(x-2)^3}\, dx=Q\\\\\frac{x^3-6x^2+13x-7}{(x+1)(x-2)^3}=\frac{A}{x+1}+\frac{B}{(x-2)^3}+\frac{C}{(x-2)^2}+\frac{D}{x-2}\\\\x^3-6x^2+13x-7=A(x-2)^3+B(x+1)+C(x+1)(x-2)+D(x+1)(x-2)^2\\\\x=-1:\; A=\frac{-1-6-13-7}{(-3)^3}=\frac{-27}{-27}=1\\\\x=2:\; B=\frac{8-24+26-7}{2+1}=\frac{3}{3}=1\\\\x^3\; |\; A+D=1\; \; ,\; \; 1+D=1\; ,\; D=0\\\\x^0\; |\; -8A+B-2C+4D=-7\; ,\; -8+1-2C=-7\; ,\; C=0\\\\\\Q=\int \Big (\frac{1}{x+1}+\frac{1}{(x-2)^3}\Big )\, dx=ln|x+1|+\frac{(x-2)^{-4}}{-4}+C=$

$=ln|x+1|-\frac{1}{4(x-2)^4}+C\; ;$

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Математика, 1 год назад

(200 000 -2•a - 20 000). 150, если а = 89997...

Геометрия, 1 год назад

Доведіть, що найбільша діагональ правильного шестикутника ділить його на дві трапеції.

Химия, 1 год назад

Задача 1. Какое количество вещества соответствует 284 г сульфат натрия NA2SO4? Задача 2. Найдиье массу и число молекул при н.у. для 11,2 л кислорода...