имеется 600 м проволоки для ограждения 6 одинаковых загонов для скота прямоугольной формы. Найди размеры 1 загон, при котором площадь загона примет максимальное значение. Найди площадь одного закона.
Приложения:

Ответы на вопрос
Ответил mathkot
0
Ответ:
Длинна 75 м
Ширина 50 м
Площадь большого загона 22 500 м²
Объяснение:
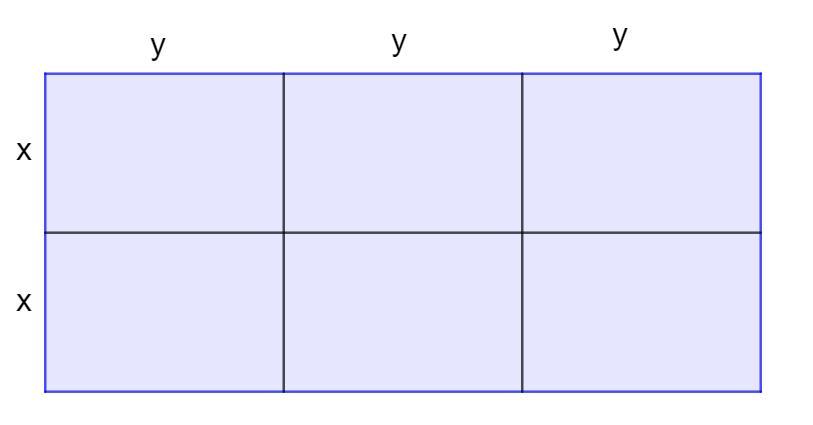
Пусть стороны маленьких загона x и y как показано на рисунке(существует единственное разбиение прямоугольника прямыми на 6 равных прямоугольников).
Периметр загона по условию 600 м, тогда:
2(2x + 3y) = 600|:2
2x + 3y = 300
3y = 300 - 2x ⇒
Пусть S - функция площади прямоугольника.
м
м
м²
Приложения:
Новые вопросы
Русский язык,
1 год назад
Другие предметы,
1 год назад
История,
2 года назад
Окружающий мир,
2 года назад
Математика,
8 лет назад