хотя бы пятое, ну а если с шестым поможете то вы мой спаситель
Приложения:
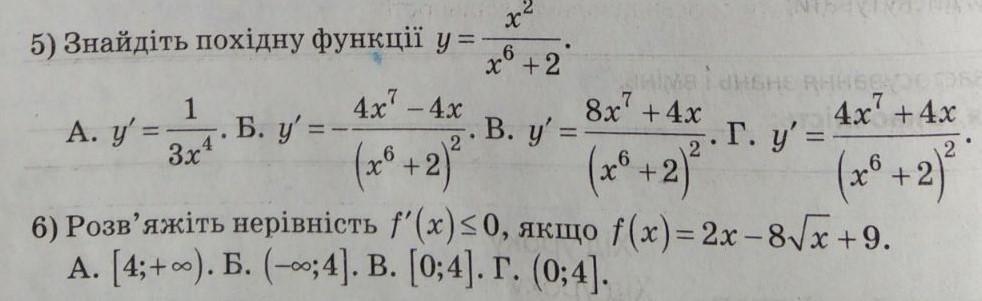
Ответы на вопрос
Ответил natalyabryukhova
3
Ответ:
5) ; Ответ Б)
6) x ∈ (0; 4]
Ответ Г)
Объяснение:
5) Найти производную функции:
Производная частного:
Используем формулы:
Ответ Б)
6) Решить неравенство f'(x) ≤ 0, если f(x) = 2x - 8√x+ 9.
Найдем производную:
Решим неравенство:
ОДЗ:
- Подкоренное выражение неотрицательно.
⇒ х ≥ 0
- На ноль делить нельзя.
⇒ х > 0
- Дробь отрицательна, если числитель и знаменатель имеют разные знаки.
Так как √х > 0 ⇒ 2√x - 4 ≤ 0
2√x ≤ 4 |:2
√x ≤ 2
x ≤ 4
Объединим с ОДЗ:
⇒ x ∈ (0; 4]
Ответ Г)
bb573878:
пересечем с одз...
Новые вопросы
Русский язык,
1 год назад
Русский язык,
1 год назад
Английский язык,
6 лет назад
Українська мова,
6 лет назад
География,
8 лет назад