Геометрия, вопрос задал prinses02 , 10 лет назад

Хорда окружности равна 6 корень из 2 и стягивает дугу в 90 градусов. Найдите длину дуги и площадь соответствующего сектора.

Ответы на вопрос

Ответил Nennn

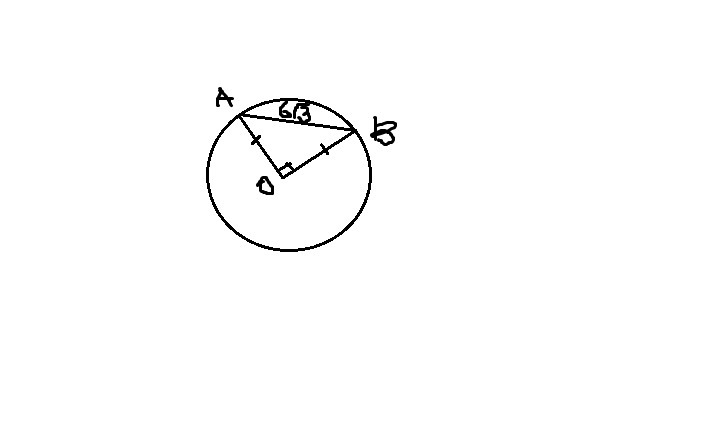
Рассмотрим треугольник АВО. Он равнобедренный, т.к. ОА и ОВ - радиусы. ∠ОАВ=∠ОВА=(180-90)/2=45°. По теореме синусов:
$frac{AO}{sinOBA} = frac{AB}{sinAOB} \ frac{r}{sin45} = frac{6 sqrt{2} }{sin90} \ frac{r}{ frac{ sqrt{2} }{2} } =6 sqrt{2} \r=frac{ sqrt{2} }{2}*6 sqrt{2}=6$ .
Площадь сектора:
$S_ alpha = frac{ alpha }{360} pi r^2\S_{90}= frac{90}{360} pi *36=9 pi$
Длина дуги сектора:
$l_ alpha = frac{ alpha }{360} *2 pi r\l_{90}= frac{90}{360} *2 pi *6=3 pi$

Приложения:

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Математика, 6 лет назад

3(-6+0,6x)+3(4-2,1x)=-24,9 Решите пожалуйста...

История, 6 лет назад

Який період в історії Франції отримав назву "республіка герцогів" А) 1870--1899 рр. Б)1871--1879 рр. В) 1875--1899 рр. Г)1879--1914 рр.

Математика, 10 лет назад

Площадь первого поля 56га.второго-60га.На первом поле высеяли семян ржи на 442кг меньше,чем на втором.Сколько килограммов семян высеяли на каждом поле? ...

Математика, 10 лет назад

На экскурсию поехали 100 школьников. В большой автобус сели 40 школьников,а остальные поровну в 3 маленьких автобуса.Сколько школьников было в каждом маленьком автобусе?

Алгебра, 10 лет назад

По пенсионному вкладу банк выплачивает 12% годовых. По истечении каждого года эти проценты капитализируются, т.е начисленная сумма присоеденяется к вкладу. На данный вид вклада был открыт счет в 80...

Биология, 10 лет назад

С изменением температуры меняется и объём воздуха: верно или неверно.