Математика, вопрос задал андрей2045 , 1 год назад

Хлопцы я в ступоре, помогите решить это недоразумение

Приложения:

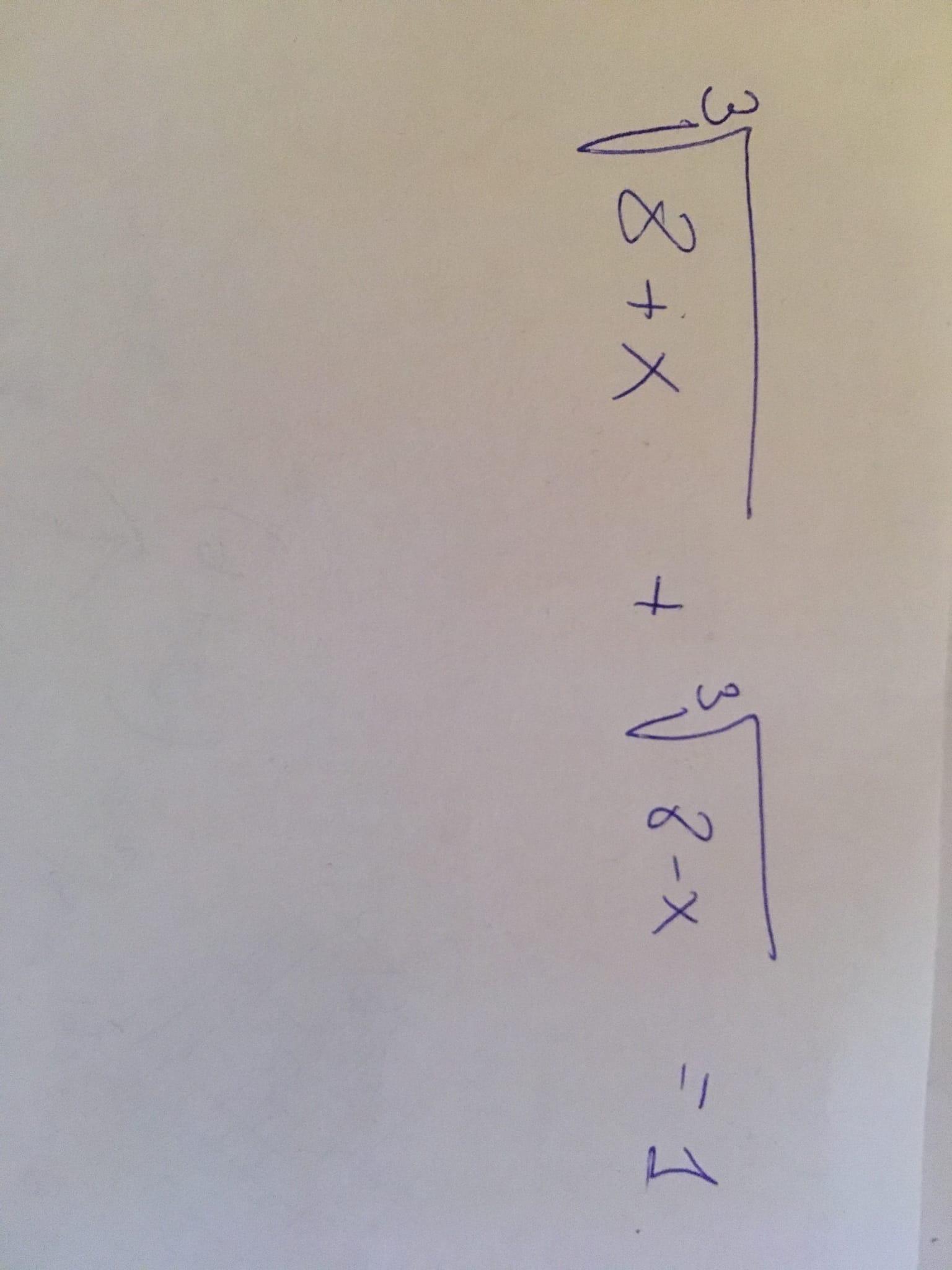
Ответы на вопрос

Ответил axatar

Ответ:

$x_{1} =8+(\frac{-1-\sqrt{21}}{2} )^{3}\\\\x_{2} =8+(\frac{-1+\sqrt{21}}{2} )^{3}$

Пошаговое объяснение:

$\sqrt[3]{8+x}+ \sqrt[3]{8-x}=1\\\sqrt[3]{x+8}- \sqrt[3]{x-8}=1\\\sqrt[3]{x+8}=1+\sqrt[3]{x-8}\\(\sqrt[3]{x+8})^{3}=(1+\sqrt[3]{x-8})^{3}\\x+8=1^{3}+3*1^{2}*\sqrt[3]{x-8}+3*(\sqrt[3]{x-8})^{2}+x-8\\1+3*\sqrt[3]{x-8}+3*(\sqrt[3]{x-8})^{2}+x-x-8-8=0\\3*(\sqrt[3]{x-8})^{2}+3*\sqrt[3]{x-8}-15=0\\(\sqrt[3]{x-8})^{2}+\sqrt[3]{x-8}-5=0$

$y=\sqrt[3]{x-8}: \\y^{2}+y-5=0\\D=1-4*1*(-5)=1+20=21\\y_{1} =\frac{-1-\sqrt{21}}{2} \\\sqrt[3]{x_{1} -8}=\frac{-1-\sqrt{21}}{2} \\x_{1} =8+(\frac{-1-\sqrt{21}}{2} )^{3}\\y_{2} =\frac{-1+\sqrt{21}}{2}\\\sqrt[3]{x_{2} -8}=\frac{-1+\sqrt{21}}{2} \\x_{2} =8+(\frac{-1+\sqrt{21}}{2} )^{3}$

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Математика, 1 год назад

4. Решите задачу с помощью составления уравнения: Сумма двух чисел равна 17, а разность их квадратов составляет 85. Найдите эти числа...

Українська література, 1 год назад

хто запропонував грати у фараонів "Тореадори з Васюківки"...

Английский язык, 1 год назад

пж помогите с англ пжпжпж ...

Литература, 1 год назад

Отгадайте пожалуйста ребус.

ОБЖ, 6 лет назад

що означає вислів день і ніч...

Математика, 6 лет назад

можете помочь математика 3 класс...