Алгебра, вопрос задал jekalolban226 , 1 год назад

ХЕЛП ПОЖАЛУЙСТА 50Б.

Приложения:

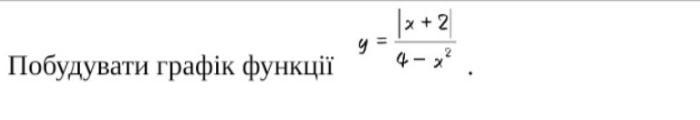
Ответы на вопрос

Ответил natalyabryukhova

Ответ:

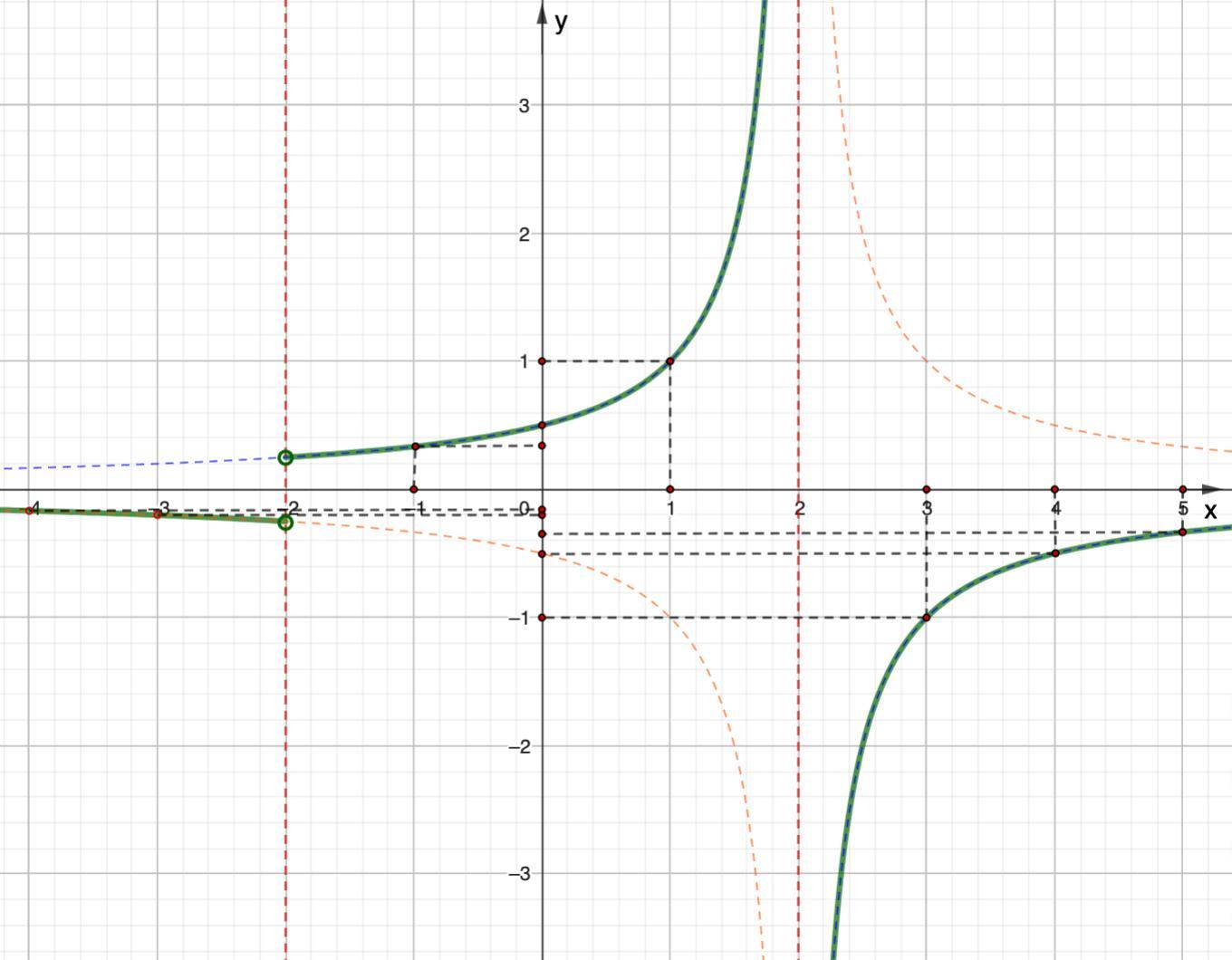
График построен.

Объяснение:

Постройте график функции:

$\displaystyle \bf y=\frac{|x+2|}{4-x^2}$

D(y) : 4 - х²≠ 0 ⇒ (2 - x)(2 + x) ≠ 0 ⇒ x ≠ ±2

Раскрытие модуля:
Модуль положительного числа - само число, модуль отрицательного числа - число противоположное.

$\displaystyle \bf |a|=\left \{ {{a,\;\;\;a\geq 0} \atop {-a,\;\;\;a < 0}} \right.$

1) x + 2 > 0 ⇒ x > -2

Тогда функция будет выглядеть так:

$\displaystyle \bf y=\frac{x+2}{(2-x)(2+x)}=\frac{1}{2-x}$

2) x + 2 < 0 ⇒ x < -2

Тогда функция будет выглядеть так:

$\displaystyle \bf y=\frac{-x-2}{(2-x)(2+x)}=-\frac{1}{2-x}$

Получили кусочную функцию:

$\displaystyle \bf y=\left \{ {{\frac{1}{2-x},\;\;\;\;\;x > -2 } \atop {-\frac{1}{2-x} ,\;\;\;\;\;x < -2}} \right.$

Построим график.

1) Промежуток (-2; +∞)

$\displaystyle \bf y=\frac{1}{2-x}$

- функция обратной пропорциональности, график - гипербола.

$\displaystyle\arraycolsep=0.7em\begin{array}{ | c | c |c|c|c| c|c|}\cline{1-7}x& -1 & 0 & 1& 3 & 4& 5 \\\cline{1-7}y& \frac{1}{3} & \frac{1}{2} & 1& -1 & -\frac{1}{2} & -\frac{1}{3} \\\cline{1-7}\end{array}$

2) Промежуток (-∞; -2)

$\displaystyle \bf y=-\frac{1}{2-x}$

- функция обратной пропорциональности, график - гипербола.

$\displaystyle\arraycolsep=0.7em\begin{array}{ | c | c |c| }\cline{1-3}x& -3 & -4 \\\cline{1-3}y& -\frac{1}{5} & -\frac{1}{6} \\\cline{1-3}\end{array}$