Геометрия, вопрос задал amir36mm53 , 6 лет назад

хелп плс
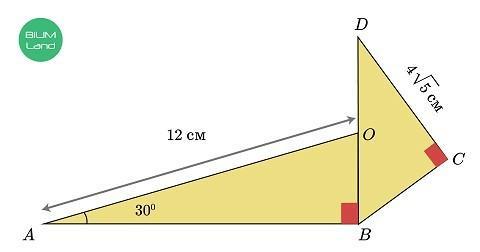
На рисунке даны два прямоугольных треугольника: ∆AOB и ∆BCD. Точка O – середина BD, AO = 12 см, DC=4√5см, ∠OAB=30°
Найди
sin∠BDC

Приложения:

Ответы на вопрос

Ответил Universalka

В Δ- ке AOB катет OB лежит против угла в 30⁰ , значит :

$\displaystyle\bf\\OB=\frac{1}{2} AO=\frac{1}{2}\cdot 12=6$

Точка O - середина BD , значит BD = 2 * OB = 2 * 6 = 12

По теореме Пифагора из Δ BDC :

$\displaystyle\bf\\BC=\sqrt{BD^{2} -DC^{2} } =\sqrt{12^{2} -(4\sqrt{5} )^{2} } =\sqrt{144-80} =\sqrt{64}=8\\\\\\Sin<BDC=\frac{BC}{BD} =\frac{8}{12} =\frac{2}{3}$

amir36mm53: фенкю вери матч!!!

Universalka: Nichts zu danken

ustugovura28: не правильно

meju: СПАСИИБО БОЛЬШОЕЕЕ!!!!!!!!!!)))))))) ;*

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Химия, 1 год назад

Вычислите массовую долю йода в йодите аллюминия АlI3 и йодоводороде HI...

Математика, 1 год назад

из 100 туристов ,10 не знают ни немецкого ни французского, 75 знали немецкий,83 французский.сколько туристов знали и французский и немецкий?

Английский язык, 6 лет назад

срочно, найти слова которые написаны сбоку. для удобвста пишите ряд и линию, вроде понятно.

Физика, 6 лет назад

Поїзд завдовжки 260 м, рухаючись рівномірно, пройшов міст за 1 хв. Яка швидкість поїзда, якщо довжина моста дорівнює 340 м? Пожалуйста срочно надо...

Математика, 8 лет назад

Как определить остаток при делении произвольного натурального числа на 10?

Алгебра, 8 лет назад

Помогите пожалуйста! 311. За ответ 12 баллов!

хелп плсНа рисунке даны два прямоугольных треугольника: ∆AOB и ∆BCD. Точка O – середина BD, AO = 12 см, DC=4√5см, ∠OAB=30°Найдиsin∠BDC​

Ответы на вопрос

хелп плс
На рисунке даны два прямоугольных треугольника: ∆AOB и ∆BCD. Точка O – середина BD, AO = 12 см, DC=4√5см, ∠OAB=30°
Найди
sin∠BDC