Алгебра, вопрос задал csq52407 , 2 года назад

ХЕЕЕЕЕЕЕЕЕЕЕЕЕЕЛЛЛЛЛЛЛЛЛЛППППППППП!!!!!

Приложения:

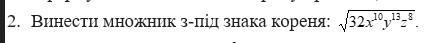
Ответы на вопрос

Ответил mic61

Ответ:

4x⁵y⁶z⁴√(2y)

Объяснение:

Воспользуемся свойством степени: √(a²ⁿ)=aⁿ

√(32x¹⁰y¹³z⁸)=√(2⁵*x¹⁰*y¹²*y*z⁸)=√(2²°²*2*x²°⁵*y²°⁶*y*z²°⁴)=2²*x⁵*y⁶*z⁴√(2*y)=

=4x⁵y⁶z⁴√(2y)

Ответил NNNLLL54

Правило: $\boxed {\ \sqrt{a^2}=|a|\ }$ .

$\sqrt{32\, x^{10}\, y^{13}\, z^8}=\sqrt{2^4\cdot 2\cdot (x^5)^2\cdot y^{12}\cdot y\cdot (z^4)^2}=\\\\\\=\sqrt{(2^2)^2\cdot 2\cdot (x^5)^2\cdot (y^{6})^2\cdot y\cdot (z^4)^2}=2^2\cdot |x^5|\cdot |\underbrace {y^6}_{\ge 0}|\cdot |\underbrace {z^4}_{\geq 0}|\cdot \sqrt{2y}=\\\\\\=4\cdot |x|^5\cdot y^6\cdot z^4\cdot \sqrt{2y}$

Так как мы не знаем знака "х", то модуль оставляем : $|x|^5=\left \{ {{-x^5\ ,\ esli\ x<0\ ,} \atop {+x^5\ ,\ esli\ x\ge 0\ .}} \right.$

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Английский язык, 1 год назад

Выпили слова в два столбика с долгим и кратким главным: see,sea,big,bridge,cheese,chips,disko,evening,fish,green,his,jeans,jeep,king,kitchen,milk,please,read,India,happy,hobby,gymnast.

Английский язык, 1 год назад

Напиши название тех фрукт и овощей, которые растут в вашей местности,в соответствии с правилами чтения буквы Аа...

Физика, 2 года назад

3. В газовом редукторе крышка крепится к корпусу болтами М6 выполненными из стали Ст3. Давление на крышку диаметром d=8 см составляет P=5 МПа. Сколько необходимо болтов, чтобы выполнялось условие не...

Алгебра, 2 года назад

помогите пожалуйста. При каком натуральном числе n указанное выражение является натуральным числом? 7n+14/n+3...

Математика, 7 лет назад

3 есеппен комек керек...

Химия, 7 лет назад

ПОМОГИТЕ ДАЮ 20 БАЛОВ!! СРОЧНО!! Ответы давайте на Ru, Ua ЯЗЫКАХ!! Ru: К раствору ферум 3 хлорида добавили раствор калий гидроксида . Выпало 0,25 моль осада. Расчитайте массу KOH в растворе луга! Ua:...