Гипотенуза равнобедренного прямоугольного треугольника принадлежит плоскости α,медиана этого треугольника,проведенная из вершины прямого угла ,образует с этой плоскостью угол 45 градусов,какой угол образует с плоскостью α катет этого треугольника.

--------------------------------------------------------------

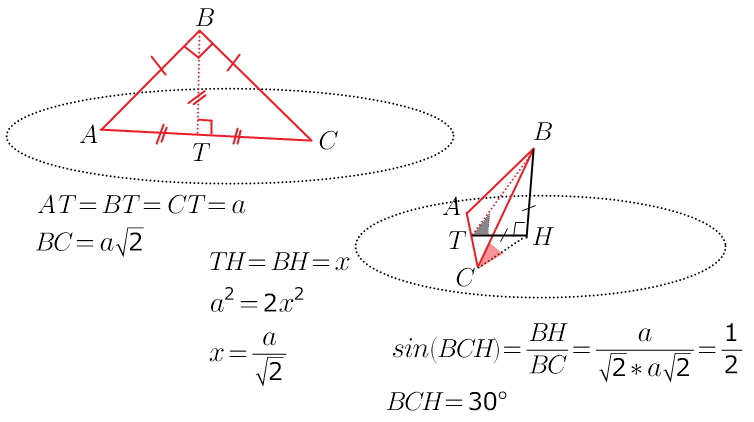
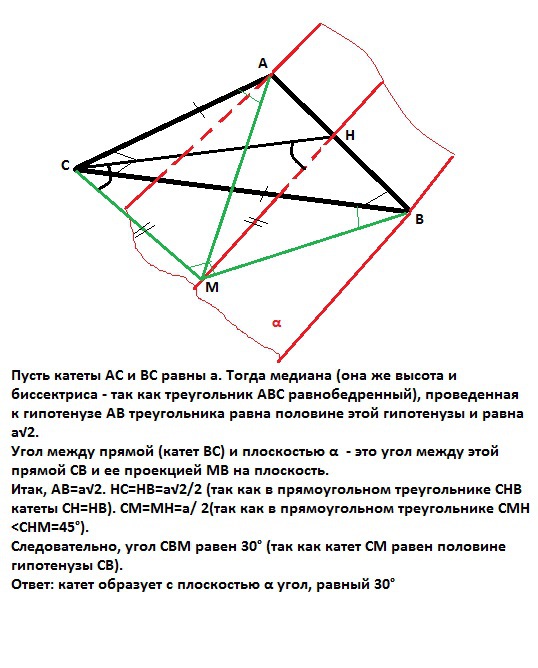
Пусть катеты АС и ВС равны а. Тогда медиана (она же высота и биссектриса - так как треугольник АВС равнобедренный), проведенная к гипотенузе АВ треугольника равна половине этой гипотенузы и равна а√2.
Угол между прямой (катет ВС) и плоскостью α  - это угол между этой прямой СВ и ее проекцией МВ на плоскость.
Итак, АВ=а√2. НС=НВ=а√2/2(так как в прямоугольном треугольнике СНВ катеты СН=НВ). СМ=МН=а/2(так как в прямоугольном треугольнике СМН <CHM=45°).
Следовательно, угол СВМ равен 30°(так как катет СМ равен половине гипотенузы СВ).
Ответ: катет образует с плоскостью α угол, равный 30°