Геометрия , задача внутри
Ответы на вопрос
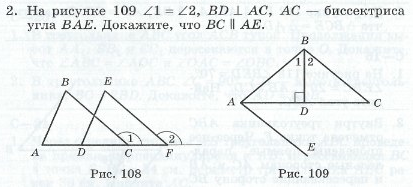
Сначало доказываем что треугольник ABC-равнобедренный
угол 1=углу 2(т.к. ВD биссектриса)
угол BDC=углу BDA(BD перпендикуляроно AC)
BD(общая сторона)
отсюда следует, что ABC-равнобедренный по второму признаку, отсюда следует что угол С= углу А
Отсюда доказываем параллельность прямых: угол С=А, а угол А=СDE (т.к АС биссектриса угла BAE) отсюда следует что BC параллельна AE(накрест лежащие углы равны)
Треугольник АВС равнобедренный, ВД - высота и биссектриса , если в треугольнике высота и биссектриса проведенные из одного угла совпадают - треугольник равнобедренный, угол ВАС=углуВСА и =углу САЕ , углы САЕ и АСВ внутренние разносторонние.Если при пересечении двух прямых третьей внутренние разносторонние углы равны, то прямые параллельны. АЕ параллельно ВС