ГЕОМЕТРИЯ ЛЕГКО МНОГО БАЛЛОВ
SABCD - правильная пирамида. точка P принадлежит ребру SD так , что SP:PD=1:2. Найдите площадь сечения пирамиды полостью, проходящей через точку P и параллельной прямым AS и CD, если SD=6, AD=3.​

Если плоскость (SAD) проходит через прямую, параллельную другой плоскости (SA||EPF), и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой (PF||SA).

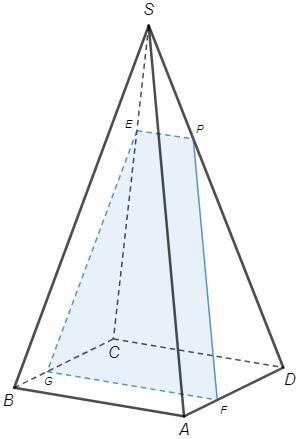
PF||SA, EP||CD. Сечение EPFG - равнобедренная трапеция.

Если продлить боковые стороны трапеции EPFG до пересечения, то получим треугольник, равный боковой грани (стороны параллельны, основания равны). Понятно, что EPFG=EPDC.

Найдем площадь боковой грани, треугольник 3,6,6

Рассмотрим подобный ему с k=2/3 треугольник 2,4,4

Его площадь по Герону =√(5*3*1*1)=√15

Тогда S(SCD)=9/4 √15

△SEP~△SCD, SP/SD=1/3 => S(SEP)/S(SCD)=1/9 => S(EPDC)/S(SCD)=8/9

S(EPDC) =8/9 *9/4 √15 =2√15