геометрия 7 класс.

Ответы на вопрос
Решение:
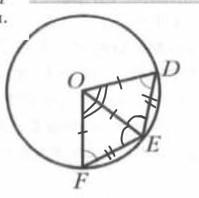
Рассмотрим ∆FOE и ∆DOE:
Так как OD и OF - радиусы => OD = OF.
∠F = ∠D, по условию.
ОЕ - общая сторона и также ОЕ = ОD = OF, так как ОЕ тоже радиус.
=> ∆FOE = DOE, по 1 признаку равенства треугольников.
=> DE = EF = 8 см.
Ответ: 8 см.
OF = OD = OE (радиусы одной окружности), следовательно, треугольники OFE и ODE - равнобедренные.
Для треугольника OFE углы у основания - ∠F = ∠E. Для треугольника ODE - ∠E = ∠D.
Так как по условию ∠F = ∠D, то также ∠OEF = ∠OED между собой. Тогда, следуя из теоремы о сумме углов треугольника, получаем что ∠OFE = ∠EOD.
Рассмотрим треугольники ОFE и ODE. OF = OD = OE (по условию), ∠OFE = ∠EOD (по выше доказанному), следовательно, треугольники ОFE = ODE по двум сторонам и углу между ними.
В равных треугольниках против равных углов лежат равные стороны. Следовательно, FE = DE = 8 см.
Ответ: 8 см.