геометрия №15
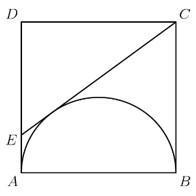
Сторона квадрата ABCD равна 2. Касательная проведенная от точки С к полуокружности с диаметром AB пересекает сторону AD в точке E. Найдите длину отрезка CE.
A 2,45
B 2,25
C 2,4
D 2,5
Приложения:
zmeura1204:
Нет такого ответа.
Ответы на вопрос
Ответил zmeura1204
2
Ответ:
СЕ=2,5 ед
Решение:
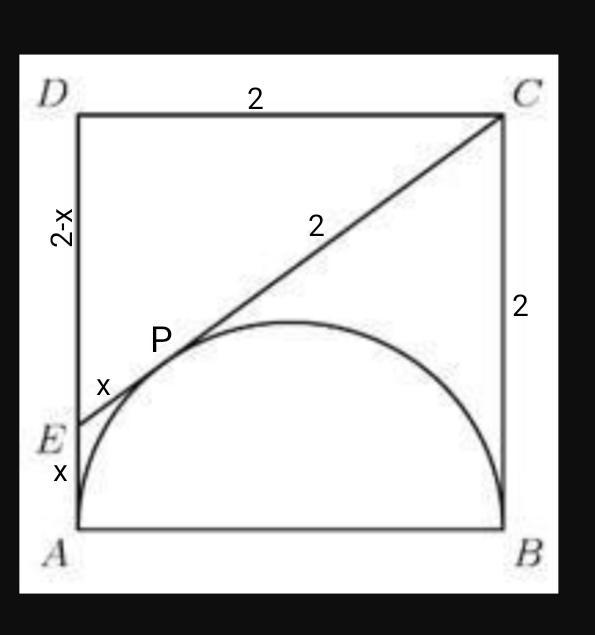
Две касательные проведенные из одной точки равны между собой.
СР=СВ=2ед.
ЕР=х; ЕР=ЕА=х.
DE=AD-EA=2-х.
СЕ=2+х
∆DEC- прямоугольный треугольник.
По теореме Пифагора
ЕС²=DC²+ED²;
Уравнение:
(2+х)²=(2-х)²+2²
4+4х+х²=4-4х+х²+4
4х+4х=4+4-4
8х=4
х=4/8
х=0,5
СЕ=2+х=2+0,5=2,5 ед.
Приложения:
спвсибо большое❤
Так ответа такого нет.
ну ладно ничего страшного, я для себя ведь знаю:)
наверное опечатка
У меня ошибка.
спасибо вам большое❤
Пожалуйста, я исправила.
https://znanija.com/task/48725526?utm_source=android&utm_medium=share&utm_campaign=question
можете с этим вопросом помочь
Новые вопросы
Русский язык,
1 год назад
Русский язык,
1 год назад
Информатика,
6 лет назад
История,
6 лет назад
Физика,
8 лет назад