Геометрия - 10 класс
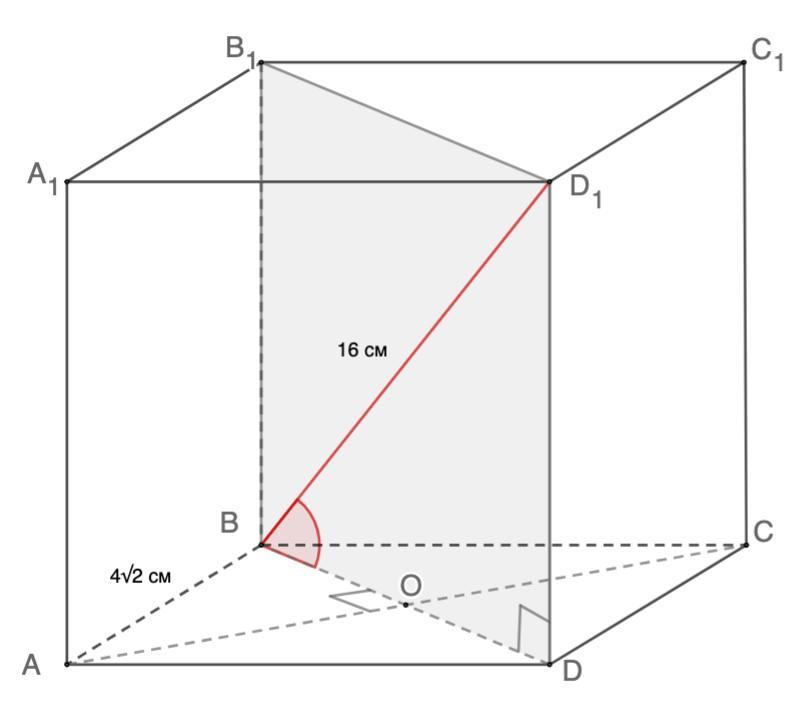
В прямоугольном параллелипеде ABCDA1B1C1D1 дано: AB=BC= 4 корень из 2, BD1=16 см. Найдите а)расстояние между прямыми BD1 и AA1 б)угол между прямой BD1 и плоскостью ABC

Ответ:

а) расстояние между прямыми BD₁ и AA₁ 4 см;

б) угол между прямой BD₁ и плоскостью (ABC) равен 60°.

Объяснение:

В прямоугольном параллелпипеде ABCDA₁B₁C₁D₁ дано: AB = BC = 4√2 см, BD₁ = 16 см. Найдите: а) расстояние между прямыми BD₁ и AA₁; б) угол между прямой BD₁ и плоскостью ABC.

Дано: ABCDA₁B₁C₁D₁ - прямоугольный параллелепипед;

AB = BC = 4√2 см, BD₁ = 16 см.

Найти: а) расстояние между прямыми BD₁ и AA₁;

б) угол между прямой BD₁ и плоскостью (ABC).

Решение:

а)  Определимся с расстоянием между прямыми BD₁ и AA₁.

• Расстояние между скрещивающимися прямыми равно расстоянию от любой точки одной из этих прямых до плоскости, проходящей через вторую прямую параллельно первой прямой.

ВВ₁ ∩ ВD₁ = B ⇒ можем провести плоскость (ВВ₁D₁).

АА₁ || BB₁;   BB₁ ⊂ (ВВ₁D₁)

• Если прямая параллельна какой либо прямой, принадлежащей плоскости, то она параллельна и самой плоскости.

⇒ АА₁ || ₁ (ВВ₁D₁)

АВСD - квадрат (по условию)

• Диагонали квадрата равны, точкой пересечения делятся пополам и взаимно перпендикулярны.

⇒ АО ⊥ BD

• Если прямая перпендикулярна плоскости, то она перпендикулярна любой прямой, лежащей в этой плоскости.

DD₁ ⊥ (АВС)   ⇒   DD₁ ⊥ АО

• Если прямая перпендикулярна двум пересекающимся прямым, лежащим в одной плоскости, то она перпендикулярна этой плоскости.

⇒ АО ⊥ (BB₁D₁)

АО - расстояние между прямыми BD₁ и AA₁.

Рассмотрим Δ ABD - прямоугольный.

По теореме Пифагора:

АВ² + AD² = BD²   ⇒   32 + 32 = BD²   ⇒   BD = 8 см.

BD = AC = 8 см   ⇒   АО = 4 см.

б)  Определим угол между прямой BD₁ и плоскостью (ABC).

Угол между прямой и плоскостью - угол между прямой и ее проекцией на данную плоскость.

BD - проекция BD₁ на (АВС)

⇒ ∠D₁BD - искомый  угол.

Рассмотрим ΔD₁BD - прямоугольный.

• Косинус угла - отношение прилежащего катета к гипотенузе.

⇒  ∠D₁BD = 60°

#SPJ1