Геометрия 10 класс
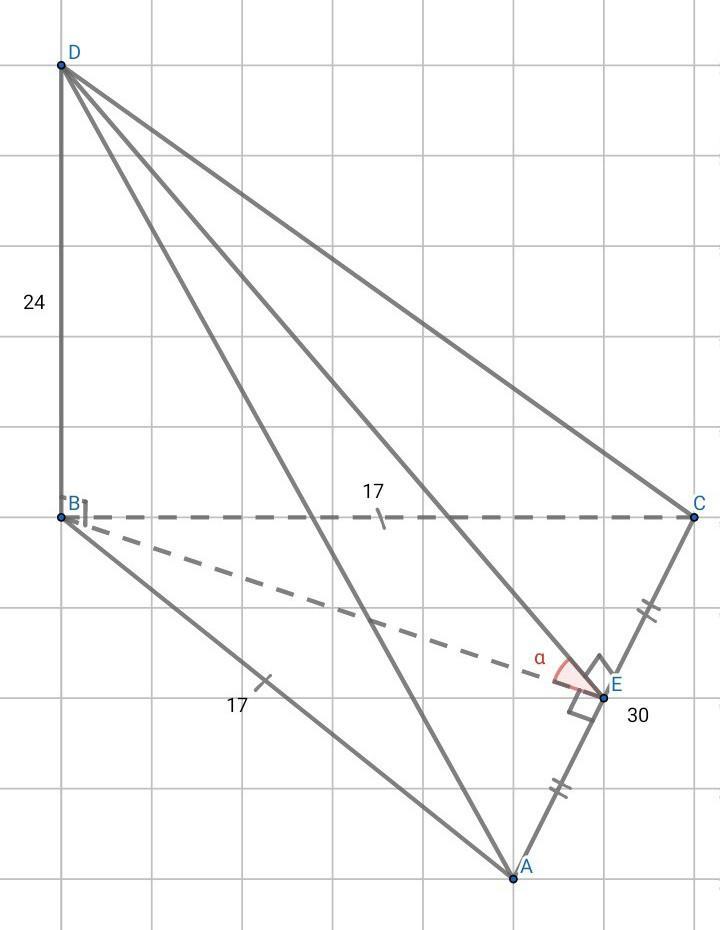
Основание пирамиды DABC – равнобедренный треугольник ABC, в котором AB = BC = 17, AC = 30 ребро BD перпендикулярно плоскости основания и равно 24. Найдите тангенс двугранного угла при ребре АС
Ответы на вопрос
Ответ:
α = arctg3 ≈ 71,57°
Объяснение:
Дано:
DABC - прямоугольная пирамида
∆АВС - равнобедренный , АВ = ВС = 17 , АС = 30
ВD⟂(АВС) , ВD = 24.
Найти:
tg∠((ACD);(ACB))
Решение:
Величина двугранного угла равна величине линейного угла. Линейный угол - это угол между двумя перпендикулярами к ребру(у нас это АС) двугранного угла, проведенными в его гранях из одной точки ребра(АС). Поэтому сделаем дополнительное построение: DE⟂AC , BE⟂AC. Таким образом искомый линейный угол - это ∠DEB. Отметим его за α .
Рассм. равнобедренный ∆АВС , высота ВЕ является ещё медианой , тогда АЕ=СЕ=30:2=15 .Найдём BE по т.Пифгора:
ВЕ = √(АВ² - АЕ²) = √(17² - 15²) = √(289 - 225) = √64 = 8
Поскольку ВD перпендикулярно плоскости основания , то она перпендикулярна любой прямой , лежащей на этой плоскости ⇒ ∆DBE - прямоугольный.
Найдём α через тангенс угла .
Тангенс острого угла в прямоугольной треугольнике равен отношению противолежащего катета к прилежащему.
tgα = DB/BE = 24/8 = 3
α = arctg3 ≈ 71,57°