Алгебра, вопрос задал chipalina99 , 1 год назад

Функция y=a^2
С 5 по 7

Приложения:

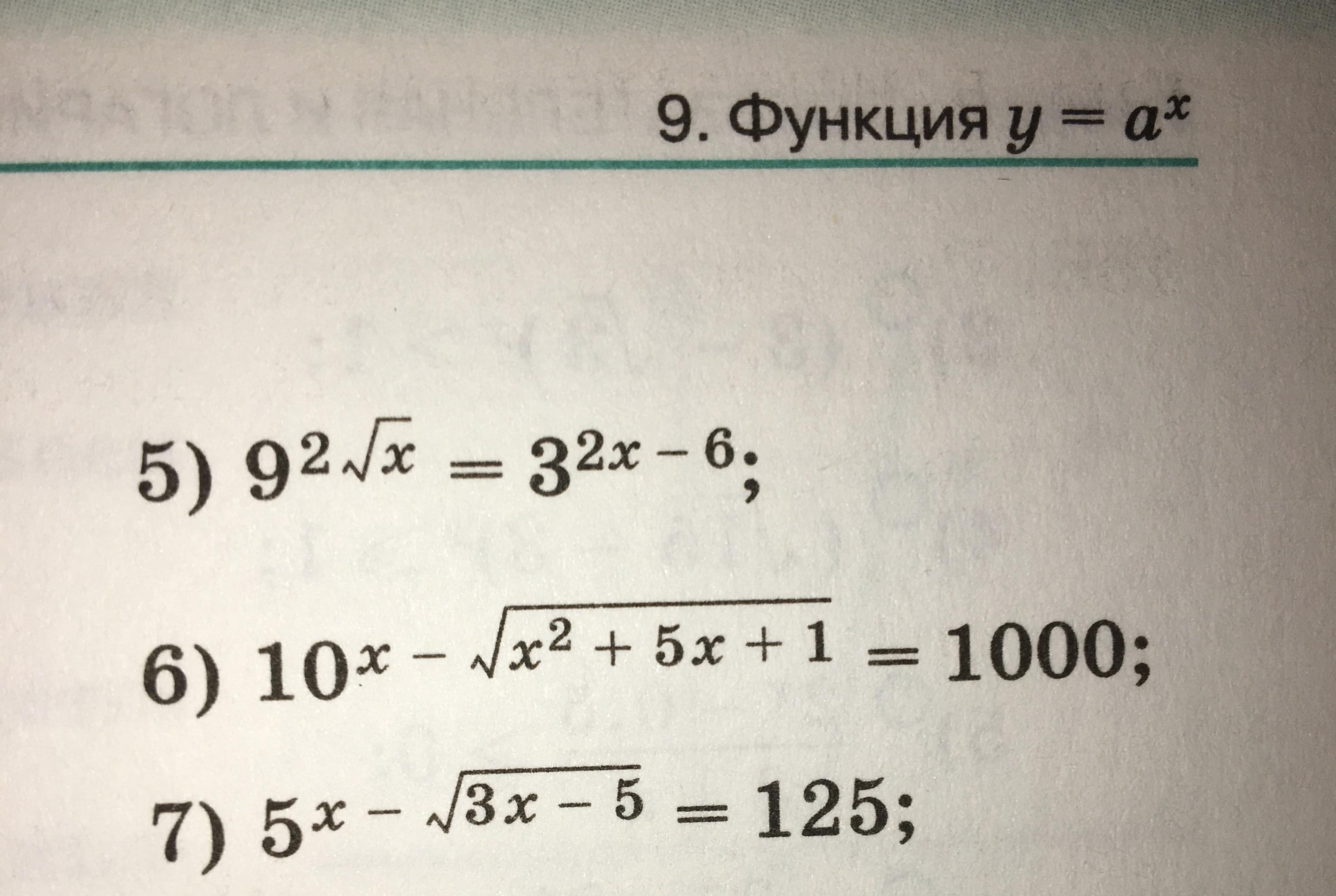
Ответы на вопрос

Ответил Arabicacoffee

Ответ:

Это 5, 6, 7

Объяснение:

Приложения:

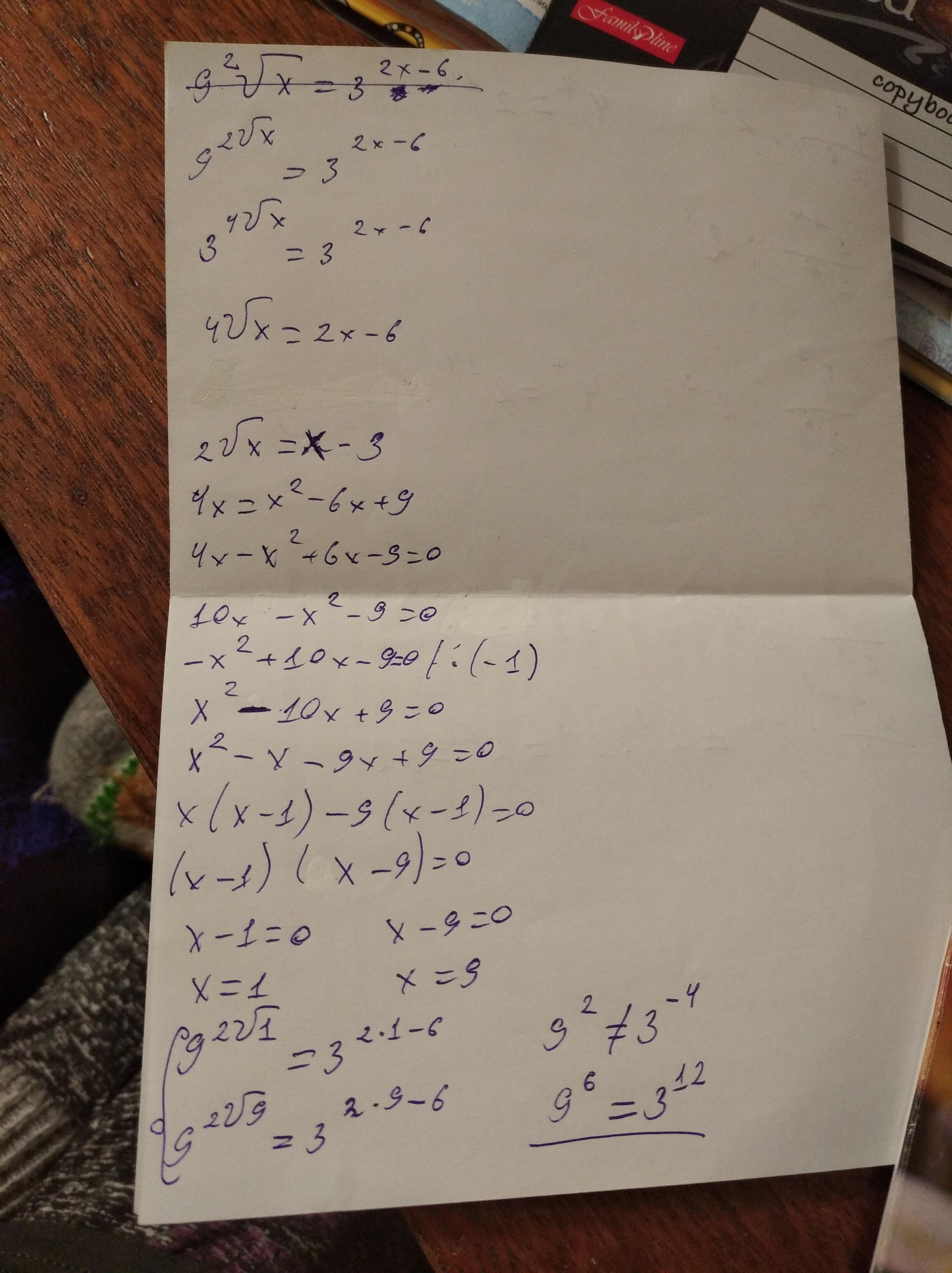
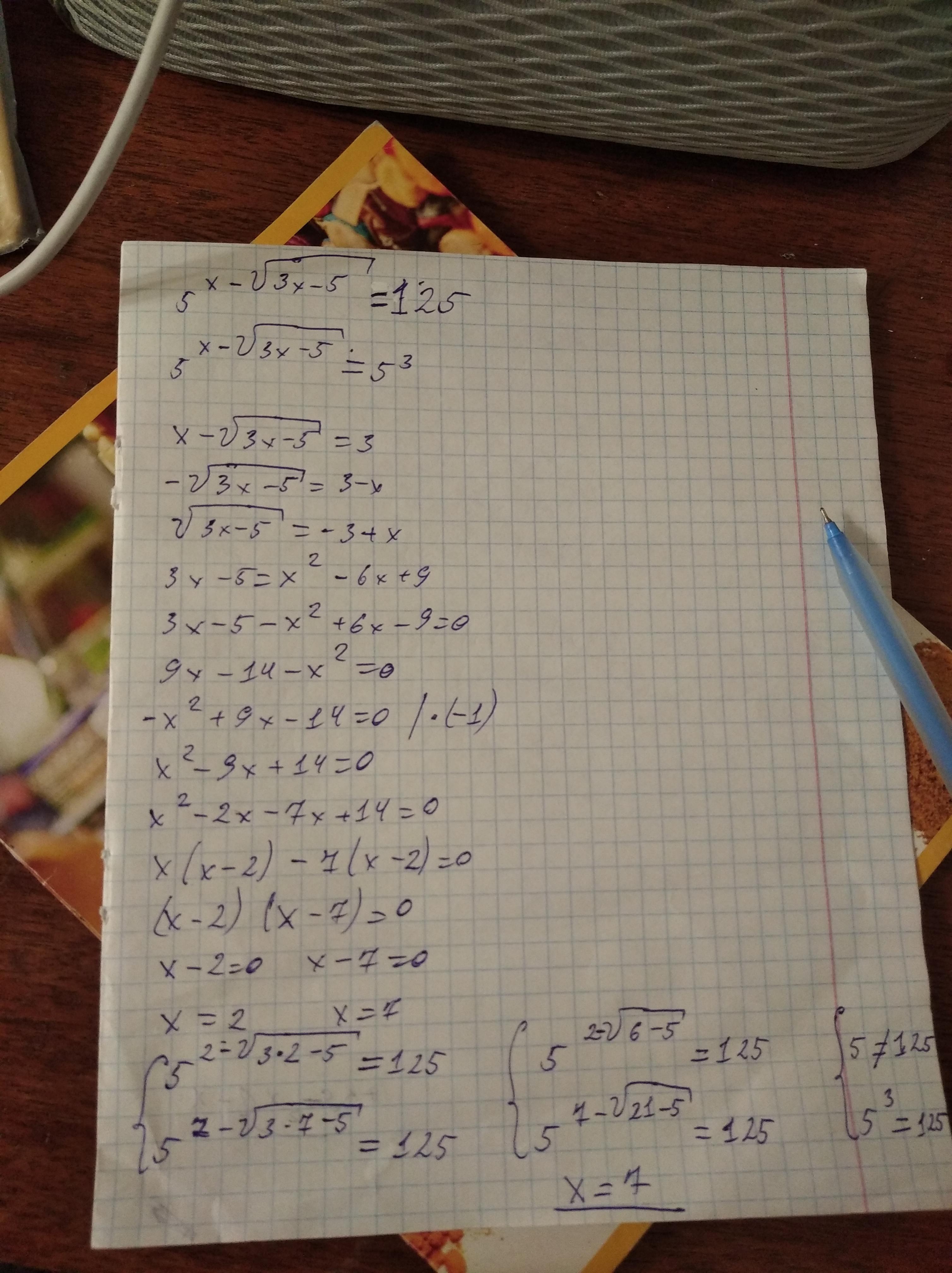
Ответил sebrithien

${3}^{4 \sqrt{x} } = {3}^{2x - 6} \\ 4 \sqrt{x} = 2x - 6 \\ 2 \sqrt{x} = - 3 \\ 4x = {x}^{2} - 6x + 9 \\ 4x - {x}^{2} + 6x - 9 = 0 \\ 10 - {x}^{2} - 9 = 0 \\ - {x}^{2} + 10x - 9 = 0 \\ {x}^{2} - 10x + 9 = 0 \\ {x}^{2} - x - 9x + 9 = 0 \\ x(x - 1) - 9(x - 1)= 0 \\ (x - 1)(x - 9) = 0 \\ x - 1 = 0 \\ x = 1 \\ x - 9 = 0 \\ x = 9$

x = 1 не является решением уравнения, так как при подстановке получается неверное равенство.

Ответ: x = 9

${10}^{x - \sqrt{ {x}^{2} + 5x + 1} } = {10}^{3} \\ x - \sqrt{ {x}^{2} + 5x + 1 } = 3 \\ - \sqrt{ {x}^{2} + 5x + 1} = 3 - x \\ \sqrt{ {x}^{2} + 5x + 1 } = - 3 + x \\ {x}^{2} + 5x + 1 = {x}^{2} - 6x + 9 \\ 5x + 1 = - 6x + 9 \\ 5x + 6x = 9 - 1 \\ 11x = 8 \\ x = \frac{8}{11}$

x = 8/11 не является решением уравнения, так как при подстановке получается неверное равенство.

${5}^{x - \sqrt{3x - 5} } = {5}^{3} \\ x - \sqrt{3x - 5} = 3 \\ - \sqrt{3x - 5} = 3 - x \\ \sqrt{3x - 5} = - 3 + x \\ 3x - 5 = {x}^{2} - 6x + 9 \\ 3x - 5 - {x}^{2} + 6x - 9 = 0 \\ 9x - 5 - {x}^{2} - 9 = 0 \\ 9x - 14 - {x}^{2} = 0 \\ - {x}^{2} + 9x - 14 = 0 \\ {x}^{2} - 9x + 14 = 0 \\ {x}^{2} - 2x - 7x + 14 = 0 \\ x(x - 2) - 7(x - 2) = 0 \\ (x - 2)(x - 7) = 0 \\ x - 2 = 0 \\ x = 2 \\ x - 7 = 0 \\ x = 7$