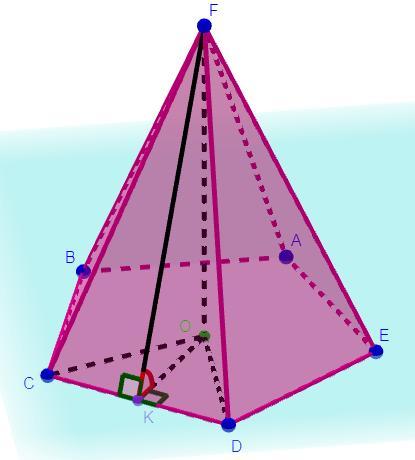
Алгебра, вопрос задал sashakikiy , 6 лет назад

FABCDE - правильная пирамида. F - вершина пирамиды, ABCDE - основание правильной пирамиды. Точка К - середина отрезка CD. Найдите площадь боковой поверхности пирамиды, если AF = 13 см. а CK = KD = 5 см. срочно дам 50 баллов геометрия

Ответы на вопрос

Ответил mathkot

Ответ:

Площадь боковой поверхности пирамиды 300 см²

Объяснение:

Дано: FABCDE - правильная пирамида, ABCDE - основание правильной пирамиды, CK = KD = 5 см, AF = 13 см

Найти: $S_{b} \ - \ ?$

Решение:

По определению правильной пирамиды в её основании лежит правильный многоугольник, а так как по условию ABCDE - основание правильной пирамиды, то ABCDE - правильный пятиугольник.

По основному свойству отрезка:

CD = CK + KD = 5 + 5 = 10 см.

Проведем отрезок FK.

По свойствам правильной пирамиды все её боковые ребра равны, тогда FA = FB = FC = FD = FE = 13 см.

Рассмотрим треугольник ΔFCD. Треугольник ΔFCD - равнобедренный, так как FC = FD. Так как по условию CK = KD, то отрезок FK - медиана. По теореме медиана равнобедренного треугольника проведённая к основанию является биссектрисой и высотой, тогда так как FK - медиана, то FK - высота, то есть FK ⊥ CD.

Рассмотрим прямоугольный треугольник ΔFCK.

По теореме Пифагора:

$FK = \sqrt{FC^{2} - KC^{2}} = \sqrt{13^{2} - 5^{2}} = \sqrt{169 - 25} = \sqrt{144} = 12$ см.