Алгебра, вопрос задал ирина150700 , 8 лет назад

f(x)=(x^2+1)/(2x-4)
Найти производную, если f'(0)

Я даже начала решать, но зашла в тупик. Есть даже ответ правильный это -1/8. Может это поможет вам в решении.

Приложения:

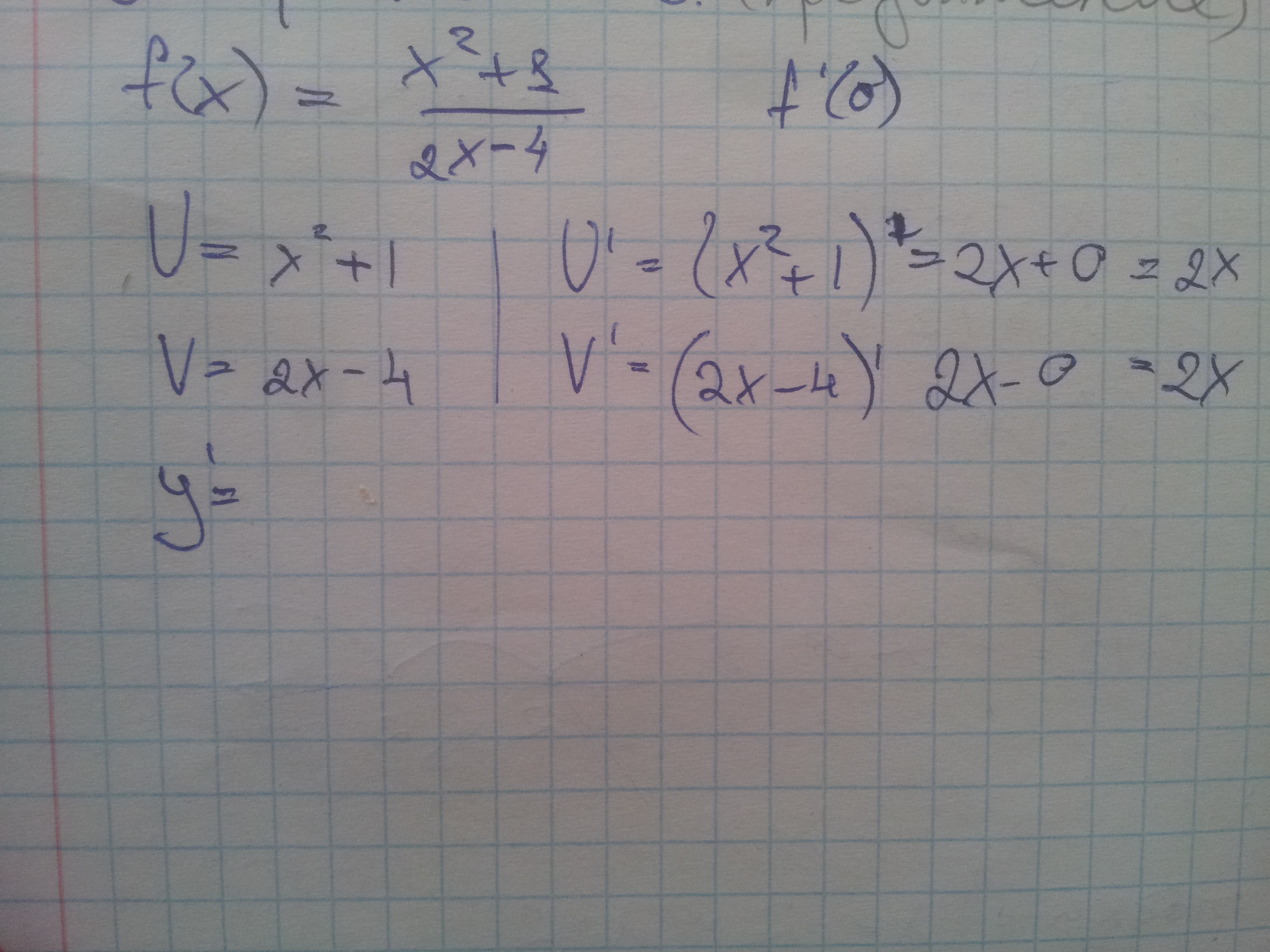
Ответы на вопрос

Ответил Аноним
0
F(x)=frac{x^2+1}{2x-4}
f'(x)=frac{2x(2x-4)-2(x^2+1)}{(2x-4)^2}=frac{4x^2-8x-2x^2-2}{(2x-4)^2}=frac{2x^2-8x-2}{(2x-4)^2}
f'(0)=frac{2*0^2-8*0-2}{(2*0-4)^2}= frac{-2}{(-4)^2} =- frac{2}{16} =- frac{1}{8}
Предыдущий вопрос
Следующий вопрос
Новые вопросы
Физика, 2 года назад
m=250 кг a=0,4m/c F-?
Английский язык, 2 года назад
помогите! По английскому языку ​...
Математика, 8 лет назад
решить задачу с помощью уравнения.Чтобы сдать в срок домашнюю контрольную работу ученик должен решать ежедневно 5 задач.Но он решал по 3 задачи в день и поэтому сдал домашнюю контрольную работу на 4...
Математика, 8 лет назад
как решить задачу? Помогите пж...
Математика, 9 лет назад
решить по действиям 650*906-161990/(152228/76-108*17)-92596 тот получит за правильный ответ 16 баллов!!
История, 9 лет назад
Помогите!!! Срочно нужно написать сочинение на тему Я в средневековой деревне (9-12 предложений)...