Алгебра, вопрос задал Wildernis , 7 лет назад

Это просто какой-то капец... Решите и это, пожалуйста:
4tgx - 3ctgx + 11 = 0.
Дедлайн до завтрашнего утра......

Ответы на вопрос

Ответил Жруся

Вот решение с помощью замены

Приложения:

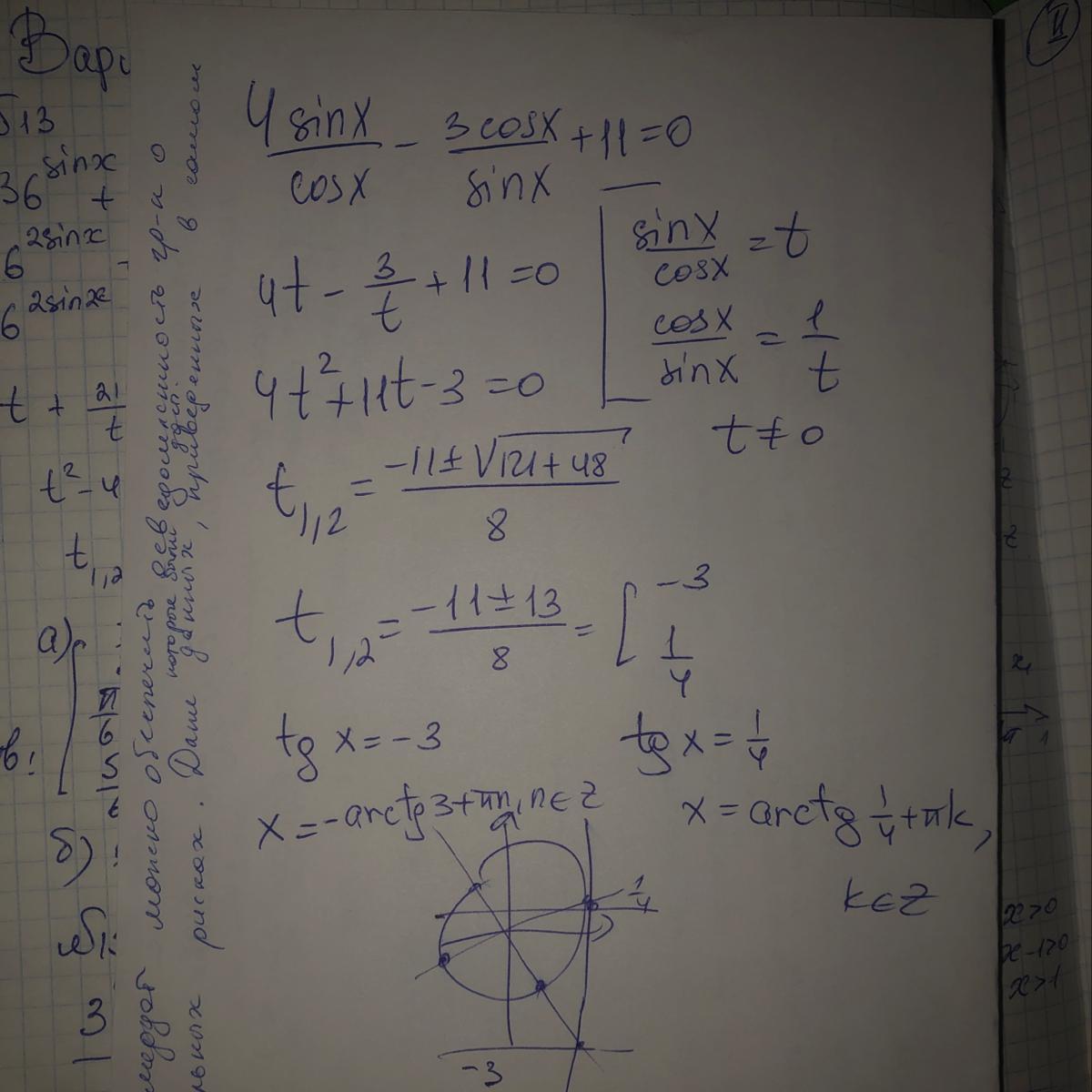
Ответил Wildernis

Спасибо за приятный разговор)))) Постараюсь больше времени уделять этой алгебре, хоть у меня его в облом и так... Удачи вам!!))

Ответил nikebod313

$4,text{tg} , x - 3 , text{ctg}, x + 11 = 0$

Так как $text{tg} , x cdot text{ctg} , x = 1$ , то $text{ctg} , x = dfrac{1}{text{tg} , x}$

$4,text{tg} , x - dfrac{3}{text{tg} , x} + 11 = 0$

Сделаем соответствующую замену: $text{tg} , x = t$

$4t - dfrac{3}{t} + 11 = 0$

$dfrac{4t^{2} + 11t - 3}{t} = 0$

$displaystyle left { {{4t^{2} + 11t - 3 = 0} atop {t neq 0 }} right.$

$4t^{2} + 11t - 3 = 0$

$D = 11^{2} - 4 cdot 4 cdot (-3) = 121 + 48 = 169$

$t_{1} = dfrac{-11 + 13}{8} = dfrac{2}{8} = dfrac{1}{4}$

$t_{2} = dfrac{-11 - 13}{8} = -dfrac{24}{8} = -3$

Обратная замена:

$1) text{tg} , x = dfrac{1}{4}$

$x = text{arctg} , dfrac{1}{4} + pi n, n in Z$

$2) text{tg} , x = -3$

$x = -text{arctg} , 3 + pi k, k in Z$

Ответ: $x = text{arctg} , dfrac{1}{4} + pi n; x = -text{arctg} , 3 + pi k; n,k in Z$

Приложения:

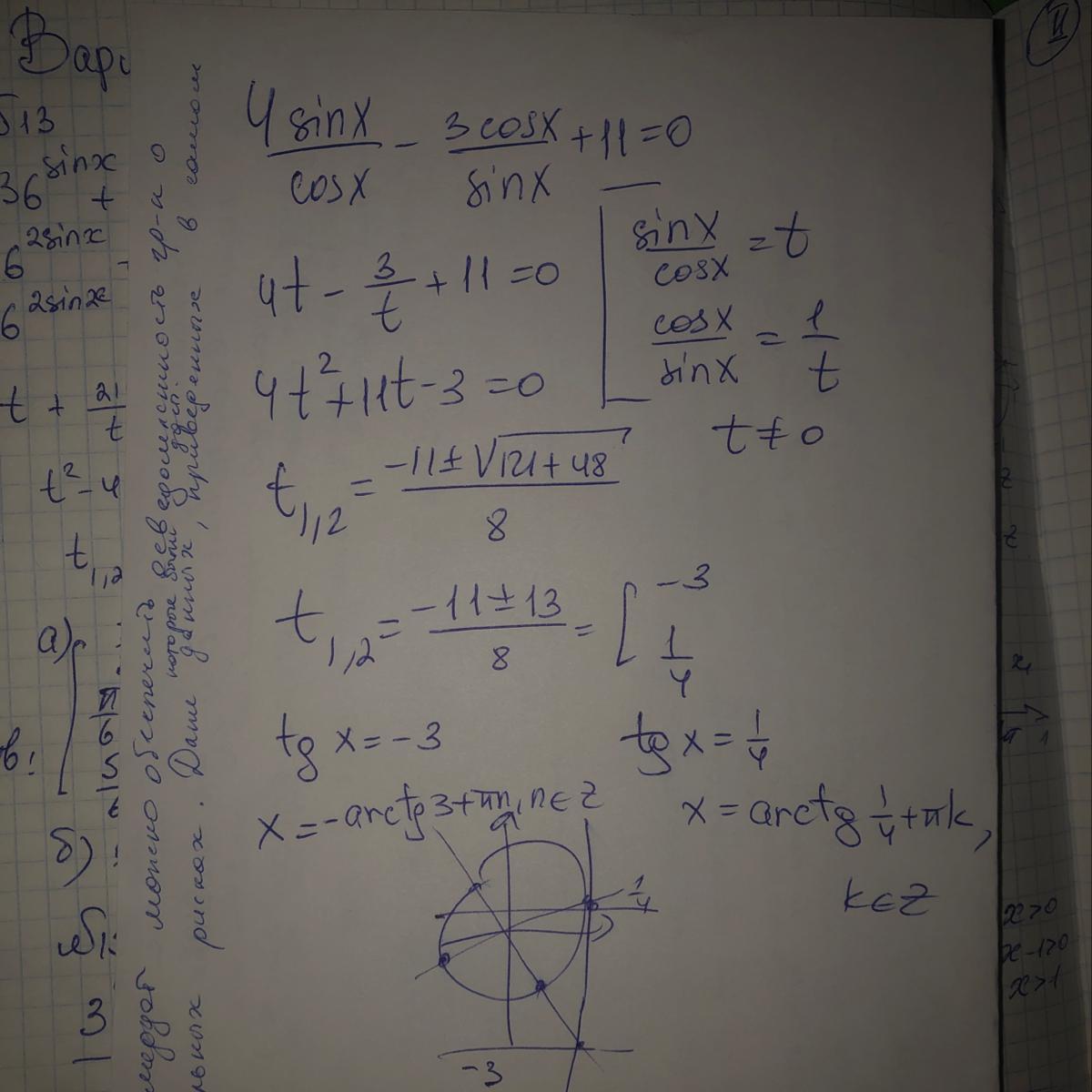
Ответил Wildernis

Все я поняла наконец-то как такое решать. Спасибо огромное

Новые вопросы

Русский язык, 1 год назад

Русский язык, 1 год назад

Математика, 7 лет назад

Литература, 7 лет назад

Физика, 8 лет назад

Математика, 8 лет назад