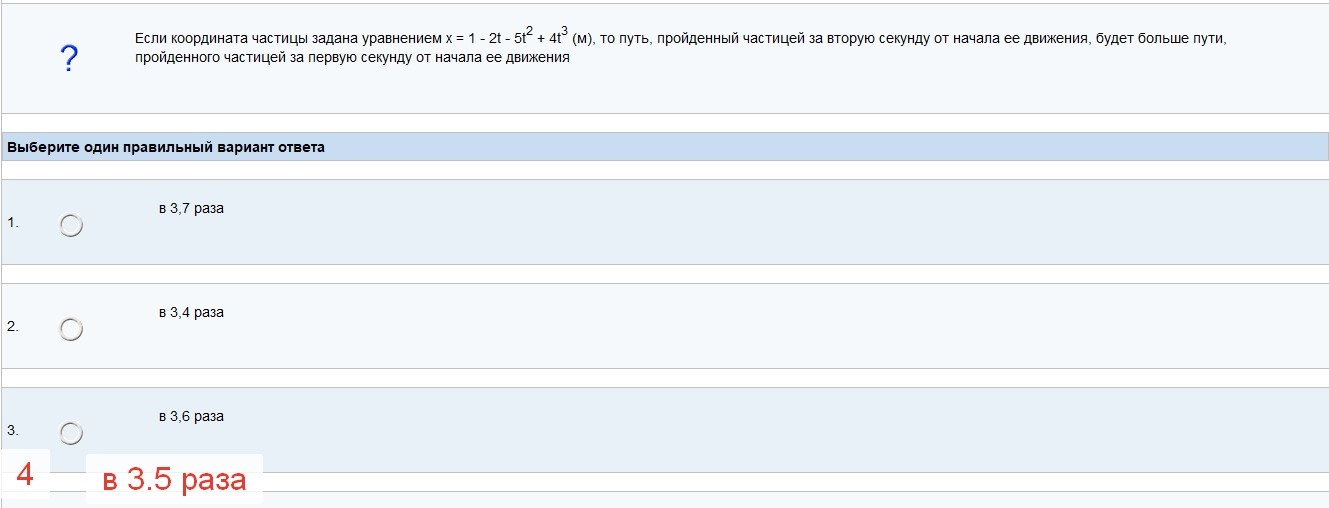
Если координата частицы задана уравнением x= 1 - 2t - 5t^2 - 4t^3, то путь, пройденный частицей за 2ю секунду от начала ее движения, будет больше пути, пройденного частицей за первую секунду от начала ее движения

Тело сначала едет против оси X (слагаемые с первой и второй степенями времени имеют знак минус, а вклад положительной третьей степени времени для малых начальных времён незначительный). Надо понять, когда оно повернёт. Возьмём производную от уравнения и приравняем её к нулю, чтобы найти его экстремумы (точки, в которых меняется направление изменения координаты, то есть направления движения):
(1 - 2*t - 5*t² + 4*t³)' = - 2 - 10*t + 12*t²
- 2 - 10*t + 12*t² = 0
6*t² - 5*t - 1 = 0
t = -1/6 (не подходит, т.к. < 0)
t = 1, значит тело двигалось одну секунду против оси X, а потом стало двигаться по направлению оси X.

За первую секунду частица прошла путь
S₁ = |x(0) - x(1)|
S₁ = |(1 - 2*0 - 5*0² + 4*0³) - (1 - 2*1 - 5*1² + 4*1³)|
S₁ = |(1) - (1 - 2 - 5 + 4)|
S₁ = |(1) - (-2)|
S₁ = 3 м.

За вторую секунду частица прошла путь
S₂ = |x(1) - x(2)|
S₂ = |(-2) - (1 - 2*2 - 5*2² + 4*2³)|
S₂ = |(-2) - (1 - 4 - 20 + 32)|
S₂ = |(-2) - (9)|
S₂ = 11 м.

Отношение S₂/S₁ = 11 м / 3 м ≈ 3,7

Спасибо. Как здесь отметить ответ, как лучший? Или он автоматически ставит?