Если каждое ребро куба увеличить на 1, то его объем увеличится на 19. Найдите ребро куба.
Ответы на вопрос
Ответил softpawskitty
0
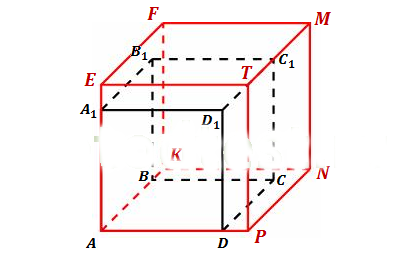
Пусть ребро AD = x ( куб ABCDA1B1C1D1), тогда АР = х + 1 (куб AKNPEFMT).Найдем объем куба ABCDA1B1C1D1 по формуле:VABCDA1B1C1D1 = AD 3 ,VABCDA1B1C1D1 = x 3 .Найдем объем куба AKNPEFMT по формуле:VAKNPEFMT = AP 3,VAKNPEFMT = (x + 1) 3.По условию задачи известно, что объем куба AKNPEFMT больше объема куба ABCDA1B1C1D1 на 19. Поэтому составим уравнение:VAKNPEFMT - VABCDA1B1C1D1 = 19,( х + 1 ) 3 - х 3 = 19.Для раскрытия скобок в левой части воспользуемся формулой куба суммы (α + b) 3 = α 3 + 3α 2 b + 3αb 3 +b 3 :x 3 + 3·x2·1 + 3·x·1 2 + 1 3 - x 3 = 19,x 3 + 3x2 + 3x + 1 - x 3 = 19,приведем подобные слагаемые:3x2 + 3x + 1 - 19 = 0,3x2 + 3x - 18 = 0.Поделим обе части уравнения на 3:x2 + x - 6 = 0.По теореме Виета найдем корни уравнения:х = - 3 ( не удовлетворяет условию, так как x > 0),x = 2.Значит ребро AD = 2.Ответ: 2.
Приложения:
Новые вопросы
Математика,
2 года назад
География,
2 года назад
Математика,
9 лет назад
Математика,
9 лет назад
Химия,
9 лет назад