Геометрия, вопрос задал Pnana , 2 года назад

ДВЕ СТОРОНЫ ТРЕУГОЛЬНИКА ОТНОСЯТСЯ КАК 3:5, А УГОЛ МЕЖДУ НИМИ 120 ГРАДУСОВ. НАЙДИ СТОРОНЫ ТРЕУГОЛЬНИКА, ЕСЛИ ЕГО ПЕРИМЕТР РАВЕН 45 ГРАДУСОВ. ПОМОГИТЕ ПЖ

Ответы на вопрос

Ответил xERISx

Уточнение к условию задачи: периметр треугольника не может измеряться в градусах.

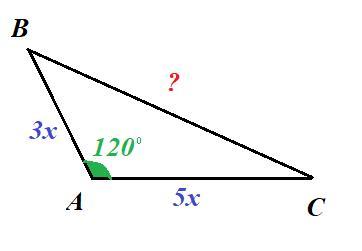
Дано: ΔABC; ∠A = 120°; AB:AC = 3:5;

$P_{\triangle ABC}=45$

Найти: AB, AC, BC

Решение:

Пусть коэффициент пропорциональности равен $x$ .

Тогда $AB=3x;\ \ AC=5x$

Периметр треугольника:

$3x+5x+BC=45;\ \ \ \ BC=45-8x$

По теореме косинусов:

$BC^2=AB^2+AC^2-2AB\cdot AC\cdot\cos120^\circ\\\\(45-8x)^2=(3x)^2+(5x)^2-2\cdot3x\cdot5x\cdot\left(-\dfrac12\right)\\\\(45-8x)^2=9x^2+25x^2+15x^2\\\\(45-8x)^2=(7x)^2\\\\|45-8x|=|7x|$

$1)~45-8x=-7x;\ \ \ x=45$ - не подходит по условию.

$2)~45-8x=7x;\ \ 15x=45;\ \ x=3$

$AB=3x=3\cdot3=9\\AC=5x=5\cdot3=15\\BC=45-(9+15)=21$

Ответ: стороны треугольника равны 9, 15 и 21.

Приложения:

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Русский язык, 1 год назад

Айжан 1саг уй тапсырмасын орындады да онын оннан бир болигиндей уакыт демалды.Айжан неше минути демалды...

Русский язык, 1 год назад

Заполни таблицу изменяя глаголы по временам...

Математика, 2 года назад

3 Есептеуді қалай орындайтыныңды түсіндір. Есепте. 9×8 000 7×90 000 45 000 : 50 45 000 : 500 32 000 : 400 32 000 : 4000...