Две самоходные баржи равномерно движутся перпендикулярно друг другу по озеру. Скорость первой V1=3м/с, V2=4м/с. На баржах установлены измерители скорости ветра. Из измерений получилось, что на первой барже скорость ветра не привышала V1, а на второй V2. Вопросы: 1)max скорость ветра относительно озера?; 2) Какой угол составляла скорость первой баржи с направлением ветра, когда скорость ветра была max относительно озёра?

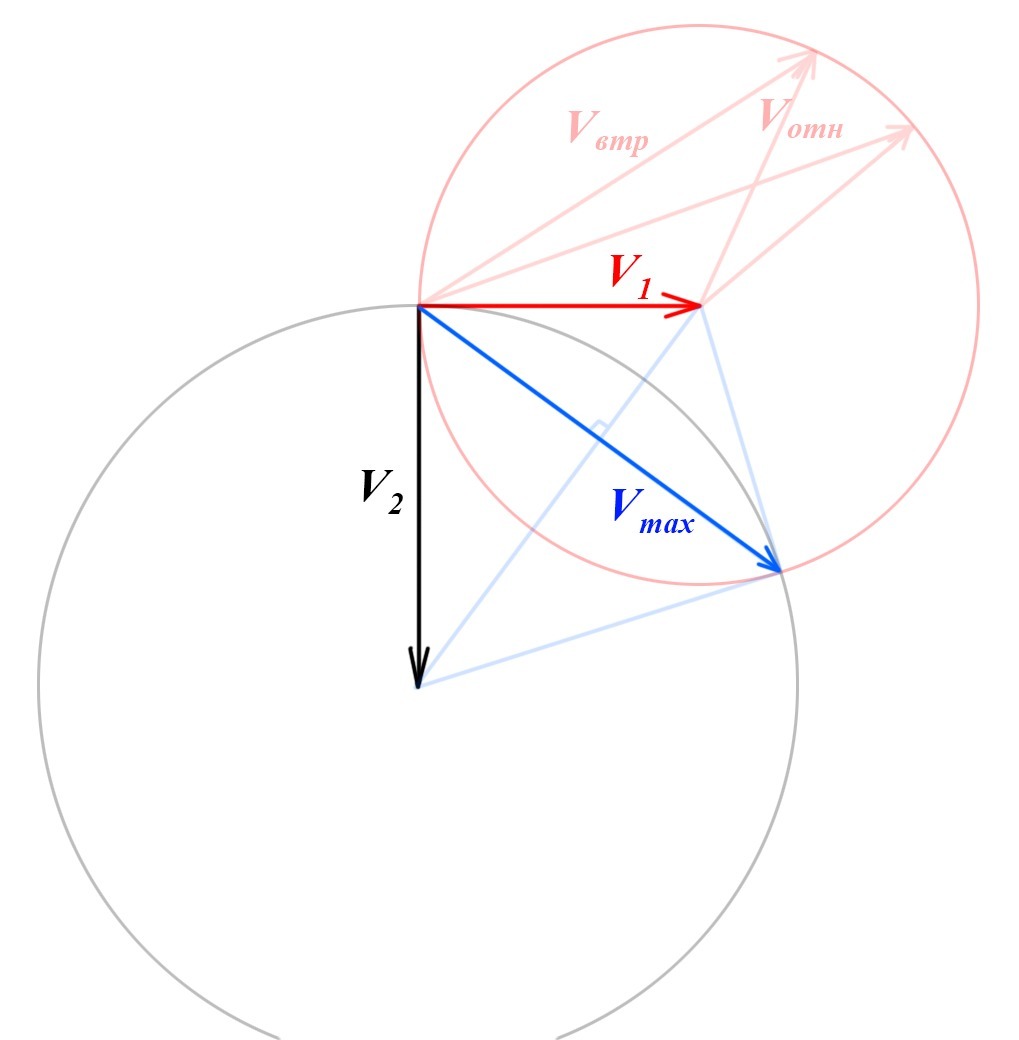
При сложении относительной скорости ветра со скоростью баржи получается собственная скорость ветра. Это показано на иллюстрации к решению задачи векторами        и    

Легко понять, что множество таких возможных векторов скорости ветра        ограниченно окружностью радиуса        с центром в конце вектора    

Аналогично можно понять, что множество тех же возможных векторов скорости ветра        ограниченно окружностью радиуса        с центром в конце вектора    

Откуда видно, что максимальная скорость ветра        определяется условиями, наложенными на множество точек возможных векторов. И её значение можно найти геометрически из прямоугольных треугольников.

Гипотенуза        прямоугольного треугольника с катетами        и        равна пяти.



Двойная площадь этого треугольника равна:



С другой стороны двойная площадь этого треугольника равна произведению гипотенузы на половину искомого вектора максимальной скорости ветра (являющуюся высотой к гипотенузе):



   –  средне-квадратично-гармоническое.

Угол между баржей и максимальным ветром найдём из того же прямоугольного треугольника, через угол между красным катетом и высотой, который из подобия равен углу между векторами        и гипотенузой        




1)       м/с

2)