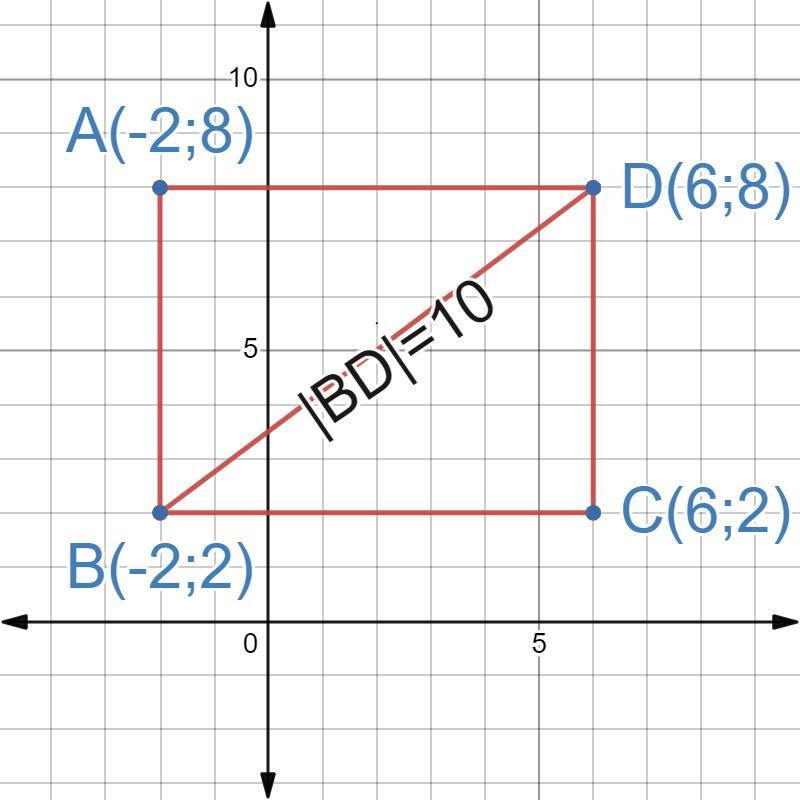
Алгебра, вопрос задал gthtvjufpfyfvb6 , 1 год назад

Дві вершини прямокутника ABCD - точки А(-2; 8) і D(6; 8). Модуль вектора BD дорівнює 10. Знайдіть координати точок B і C.

Ответы на вопрос

Ответил sangers1959

Відповідь: B(-2;2), C(6;2).

Пояснення:

A(-2;8) D(6;8) |BD|=10 B(x;y)=? C(x;y)=?

$|AD|=\sqrt{(D_x-A_x)^2+(D_y-A_y)^2}=\sqrt{(6-(-2))^2+(8-8)^2} =\\\\=\sqrt{(6+2)^2+0^2}=\sqrt{8^2+0} =8.\\$

$|AB|^2=|BD|^2-|AD|^2=10^2-8^2=100-64=36\\\\|AB|=6.$

Так як це прямокутник, координати точок B і C дорівнюють:

B(x;y)=(-2;8-6)=(-2;2).

C(x;y)=(6;8-6)=(6;2).

Приложения:

aytrtyyttty: здравствуйте, помогите пожалуйста

aytrtyyttty: прощу вас

Новые вопросы

Английский язык, 1 год назад

Алгебра, 1 год назад

Геометрия, 1 год назад

Українська мова, 1 год назад

Информатика, 6 лет назад

Химия, 6 лет назад