дві сторони трикутника дорівнюють 3 см і 8 см. Знайдіть третю сторону трикутника, якщо вона у √3 разів більша за радіус кола, описаного навколо трикутника. Скільки розв'язків має задача (написати повну відповідь)
Ответы на вопрос
Ответил KuOV
1
Ответ:
Третья сторона треугольника равна 7 см или √97 см.
Задача имеет два решения.
Объяснение:
По теореме синусов:
- отношение стороны треугольника к синусу противолежащего угла равно удвоенному радиусу описанной окружности:
По условию a = √3 · R, тогда
Так как sin ∠A = sin (180° - ∠A), то нельзя однозначно определить угол.
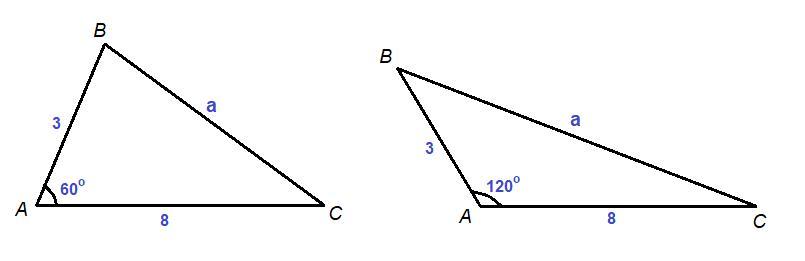
∠А = 60° или ∠А = 120°.
1. ∠А = 60°
По теореме косинусов:
a² = AB² + AC² - 2 · AB · AC · cos∠A
a = 7 см
2. ∠А = 120°
По теореме косинусов:
a² = AB² + AC² - 2 · AB · AC · cos∠A
a = √97 см
Приложения:
Ответил Аноним
1
Відповідь:
Пояснення:
фото
Приложения:

Новые вопросы
Английский язык,
1 год назад
Английский язык,
1 год назад
Математика,
6 лет назад
Русский язык,
6 лет назад
Математика,
8 лет назад