Алгебра, вопрос задал gavilon324 , 1 год назад

Довести, що при всіх допустимих значеннях змінної значення виразу не залежить від значення змінної, яка входить в нього

Доказать, что при всех допустимых значениях переменной значение выражения не зависит от входящего в него значения переменной

Приложения:

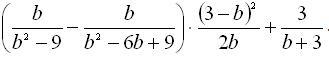
aarr04594: https://znanija.com/task/52527247

aarr04594: Ви вже цей вираз розмістили. У відповіді 0. Допишіть, що оскільки значення виразу дійсне число, то при всіх допустимих значеннях змінної значення виразу не залежить від значення змінної.

Ответы на вопрос

Ответил yanata101

$( \frac{b}{ {b}^{2} - 9} - \frac{b}{ {b}^{2} - 6b + 9} ) \times \frac{ {(3 - b)}^{2} }{2b} + \frac{3}{b + 3} = ( \frac{b}{(b - 3)(b + 3)} - \frac{b}{ {(b - 3)}^{2}} ) \times \frac{ {(3 - b)}^{2} }{2b} + \frac{3}{b + 3} = \frac{b(b - 3) - b(b + 3)}{ {(b - 3)}^{2} (b + 3)} \times \frac{ {(b - 3)}^{2} }{2b} + \frac{3}{b + 3}= \frac{b(b - 3 - b - 3)}{ {(b - 3)}^{2} (b + 3)} \times \frac{ {(b - 3)}^{2} }{2b} + \frac{3}{b + 3} = \frac{ - 6b}{ {(b - 3)}^{2} (b + 3)} \times \frac{ {(b - 3)}^{2} }{2b} + \frac{3}{b + 3} = - \frac{3}{ b + 3} + \frac{3}{b + 3} = 0$

Унаслідок спрощень виразу виходить число, тому вираз не залежить від значення змінної, що і треба було довести.

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Математика, 11 месяцев назад

БУДЬ ЛАСКА! ДУЖЕ ПОТРІБНА ДОПОМОГА! Всі сторони та висота трапеції складають арифметичну прогресію. Периметр трапеції дорівнює 40 см, площа трапеції 55 см кв. Знайти сторони та висоту трапеції.

География, 11 месяцев назад

Какое слово срочноо даю 35 балів...

Физика, 1 год назад

1)дано: U=15В R=9,25кОм t=15минута Q-?

Химия, 1 год назад

2. Загальна формула насичених амінів: А. Сn Н2 n+2 - NH2 Б. Сn Н2 n - NH2 В. Сn Н2 n+1 - NH2 Г. Сn Н2 n+1 - N...

Русский язык, 6 лет назад

ДАЮ 10 БАЛЛОВ! Разряды имен прилагательных / (скриншот ниже)...

Математика, 6 лет назад

МЕЖДУ КАКИМИ ЦЕЛЫМИ ЧИСЛАМИ заключено число на фото...