Доведіть тотожність a + a ^ 2 + (2a ^ 2 + 3a + 1)/(a ^ 2 - 1) - (a ^ 3 + 2a)/(a - 1) = - 1 СРОЧНО ДАМ 90 БАЛІВ!!
Приложения:
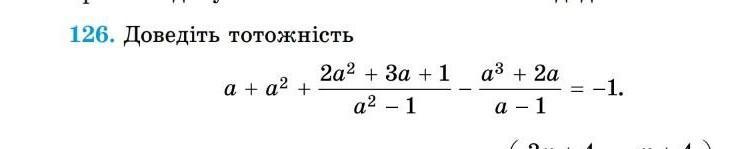
Ответы на вопрос
Ответил alexillysaltfetish
2
To solve the equation a + a^2 + (2a^2 + 3a + 1)/(a^2 - 1) - (a^3 + 2a)/(a - 1) = -1, you can follow these steps:
1. First, combine like terms and simplify the expression on the left-hand side of the equation:
a + a^2 + (2a^2 + 3a + 1)/(a^2 - 1) - (a^3 + 2a)/(a - 1) = -1
2. Factor the denominators:
a + a^2 + (2a^2 + 3a + 1)/[(a + 1)(a - 1)] - (a^3 + 2a)/(a - 1) = -1
3. Find a common denominator for the fractions:
a + a^2 + [(2a^2 + 3a + 1)(a + 1)]/[(a + 1)(a - 1)] - (a^3 + 2a)/(a - 1) = -1
4. Multiply both sides of the equation by the common denominator to eliminate fractions:
[(a + 1)(a - 1)][a] + [(a + 1)(a - 1)][a^2] + (2a^2 + 3a + 1)(a + 1) - [(a + 1)(a - 1)][(a^3 + 2a)] = -1[(a + 1)(a - 1)]
5. Expand and simplify the equation:
a(a^2 - 1) + a^2(a^2 - 1) + (2a^2 + 3a + 1)(a + 1) - (a^4 - a)(a + 1) = -1
6. Continue simplifying:
a^3 - a + a^4 - a^2 + 2a^2 + 3a + 1 - (a^5 - a^2 + a^4 - a) = -1
7. Combine like terms:
4a^4 - 2a^3 + 3a + 1 - a^5 = -1
8. Move all terms to one side of the equation:
4a^4 - 2a^3 + 3a + 1 - a^5 + 1 = 0
9. Simplify further:
4a^4 - 2a^3 - a^5 + 3a = 0
10. Factor out a common term 'a' to make it easier to factor:
a(4a^3 - 2a^2 - a^4 + 3) = 0
11. Now, set each factor equal to zero:
a = 0
4a^3 - 2a^2 - a^4 + 3 = 0
You can solve the second equation for 'a' or use numerical methods to find its solutions, as it's a cubic equation.
The solutions to the original equation are a = 0 and the roots of the second equation.
1. First, combine like terms and simplify the expression on the left-hand side of the equation:
a + a^2 + (2a^2 + 3a + 1)/(a^2 - 1) - (a^3 + 2a)/(a - 1) = -1
2. Factor the denominators:
a + a^2 + (2a^2 + 3a + 1)/[(a + 1)(a - 1)] - (a^3 + 2a)/(a - 1) = -1
3. Find a common denominator for the fractions:
a + a^2 + [(2a^2 + 3a + 1)(a + 1)]/[(a + 1)(a - 1)] - (a^3 + 2a)/(a - 1) = -1
4. Multiply both sides of the equation by the common denominator to eliminate fractions:
[(a + 1)(a - 1)][a] + [(a + 1)(a - 1)][a^2] + (2a^2 + 3a + 1)(a + 1) - [(a + 1)(a - 1)][(a^3 + 2a)] = -1[(a + 1)(a - 1)]
5. Expand and simplify the equation:
a(a^2 - 1) + a^2(a^2 - 1) + (2a^2 + 3a + 1)(a + 1) - (a^4 - a)(a + 1) = -1
6. Continue simplifying:
a^3 - a + a^4 - a^2 + 2a^2 + 3a + 1 - (a^5 - a^2 + a^4 - a) = -1
7. Combine like terms:
4a^4 - 2a^3 + 3a + 1 - a^5 = -1
8. Move all terms to one side of the equation:
4a^4 - 2a^3 + 3a + 1 - a^5 + 1 = 0
9. Simplify further:
4a^4 - 2a^3 - a^5 + 3a = 0
10. Factor out a common term 'a' to make it easier to factor:
a(4a^3 - 2a^2 - a^4 + 3) = 0
11. Now, set each factor equal to zero:
a = 0
4a^3 - 2a^2 - a^4 + 3 = 0
You can solve the second equation for 'a' or use numerical methods to find its solutions, as it's a cubic equation.
The solutions to the original equation are a = 0 and the roots of the second equation.
Новые вопросы
Физика,
11 месяцев назад
Математика,
11 месяцев назад
Математика,
11 месяцев назад
Биология,
11 месяцев назад
Другие предметы,
6 лет назад
Математика,
6 лет назад