Алгебра, вопрос задал kolokol483424 , 3 месяца назад

Доведіть Тотожність:

Приложения:

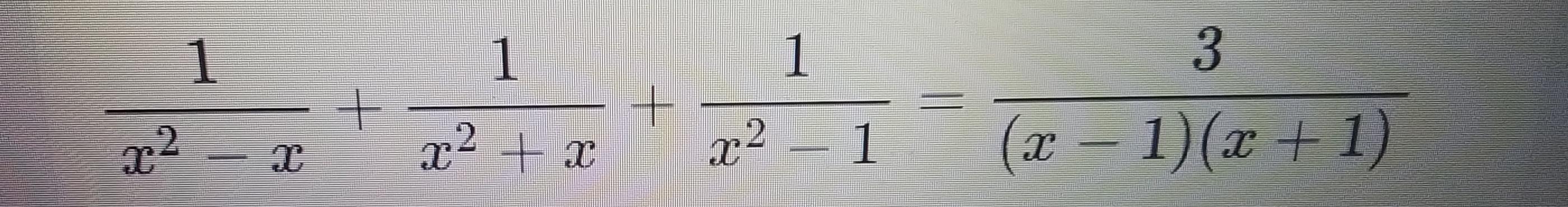
Ответы на вопрос

Ответил Ivan19074

Ответ:

Объяснение:

Разложим все знаменатели в левой части на множители:

$\frac{1}{x^2-x}+\frac{1}{x^2+x}+\frac{1}{x^2-1}=\frac{3}{(x-1)(x+1)}\\\frac{1}{x(x-1)}+\frac{1}{x(x+1)}+\frac{1}{(x-1)(x+1)}=\frac{3}{(x-1)(x+1)}\\$

Теперь сведём всё к общему знаменателю:

$\frac{1}{x(x-1)}+\frac{1}{x(x+1)}+\frac{1}{(x-1)(x+1)}=\frac{3}{(x-1)(x+1)}\\\frac{x+1}{x(x-1)(x+1)}+\frac{x-1}{(x(x-1)(x+1)}+\frac{x}{x(x-1)(x+1)}=\frac{3x}{x(x-1)(x+1)}\\x+1+(x-1)+x=3x\\3x=3x\\0=0$

Следовательно, равенство доказано.

Ответил parus77

Ответ:

Объяснение:

решение внизу

Приложения:

Предыдущий вопрос

Следующий вопрос

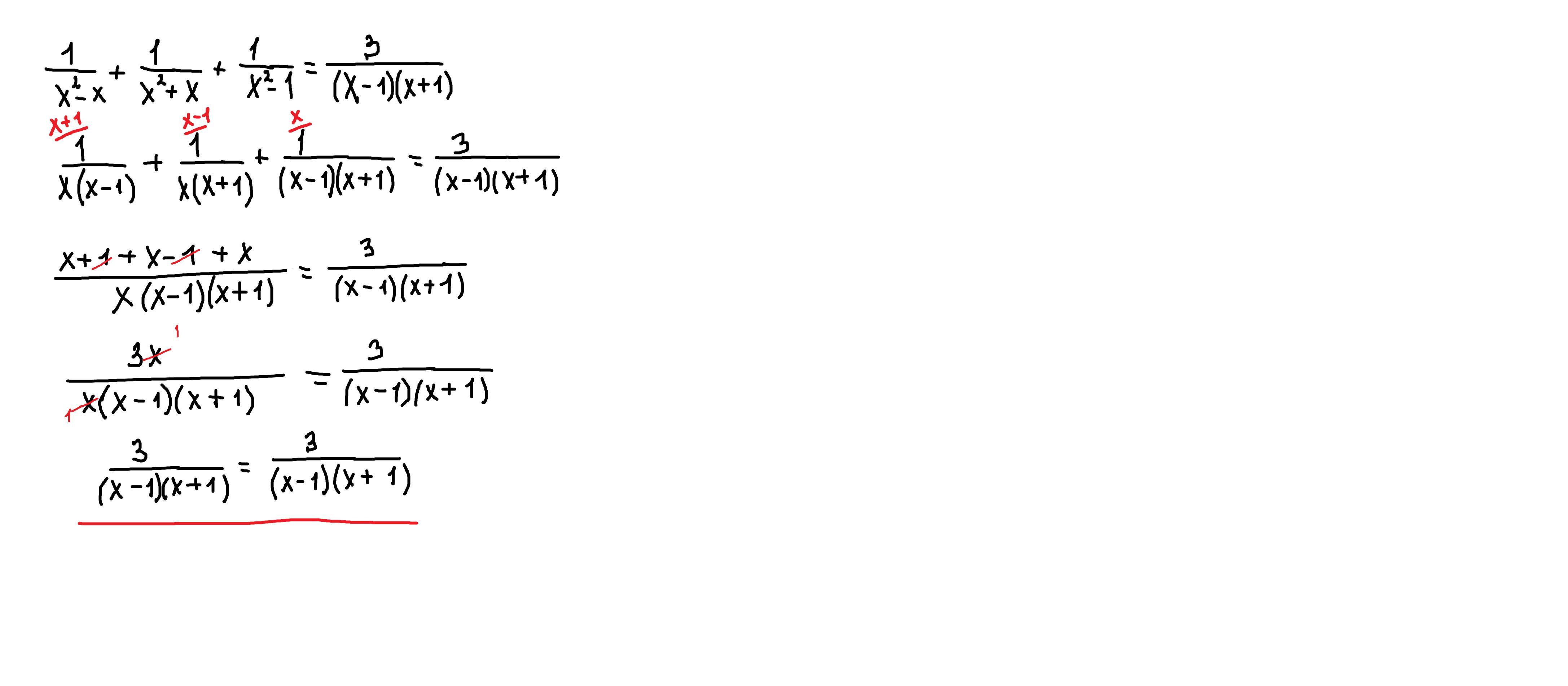
Новые вопросы

Українська мова, 2 месяца назад

Допоможіть будь-ласка...

Математика, 2 месяца назад

36z + 44 - 15z, при z = 9...

Алгебра, 3 месяца назад

Решить показательное неравенство с фото...

Алгебра, 3 месяца назад

ДОПОМОЖІТЬ!! 1.Подайте у вигляді многочлена: 1) (5y + 7)(3y -2) - 15(y² + 3) 2) (4m + m²)(5 - 7m) 2.Розв'яжіть рівняння: 1) 3x² + 9x = 0 2) (3x + 4)(x - 2) = x(3x + 2) 3) [tex] \frac{2x -...

География, 6 лет назад

Можете пожалуйста помочь с географи ей. На фото ср...

Русский язык, 6 лет назад

486 Продолжите данную тематическую группу слов. Составьте с любыми тремя словами одно повествовательное, одно вопросительное и одно побудительное предложения. Обозначьте в них грамматическую основу.