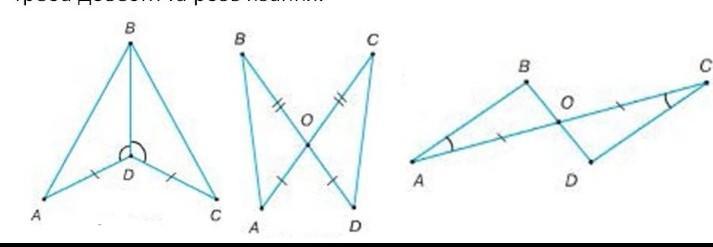
Доведіть, що трикутники на малюнках рівні. Запишіть, що дано, що треба довести та розв'язання. ​

1. Дано: ∆ABC, ∆BCD, AC = DC, кут ADB = кут CDB.

Довести: ∆ABC = ∆BCD.

Доведення:

Якщо AC = DC, BD – спільна, кут ADB = кут CDB, то ∆ABC = ∆BCD за двома сторонами та кутом між ними (перша ознака рівності трикутників). Доведено.

2. Дано: ∆AOB, ∆DOC, AO = DO, BO = CO.

Довести: ∆AOB = ∆DOC.

Доведення:

Якщо AO = DO, BO = CO, кут AOB = кут DOC (бо вертикальні кути рівні), то ∆AOB = ∆DOC за двома сторонами і кутом між ними (перша ознака рівності трикутників). Доведено.

3. Дано: ∆AOB, ∆DOC, AO = CО, кут BAO = кут DCO.

Довести: ∆AOB = ∆DOC

Доведення:

Якщо AO = CО, кут BAO = кут DCO, кут AOB = кут DOC (бо вертикальні кути рівні), то ∆AOB = ∆DOC за стороною та двома прилеглими до неї кутами (друга ознака рівності трикутників). Доведено.

Буду дуже вдячна, якщо позначите як найкраща відповідь.