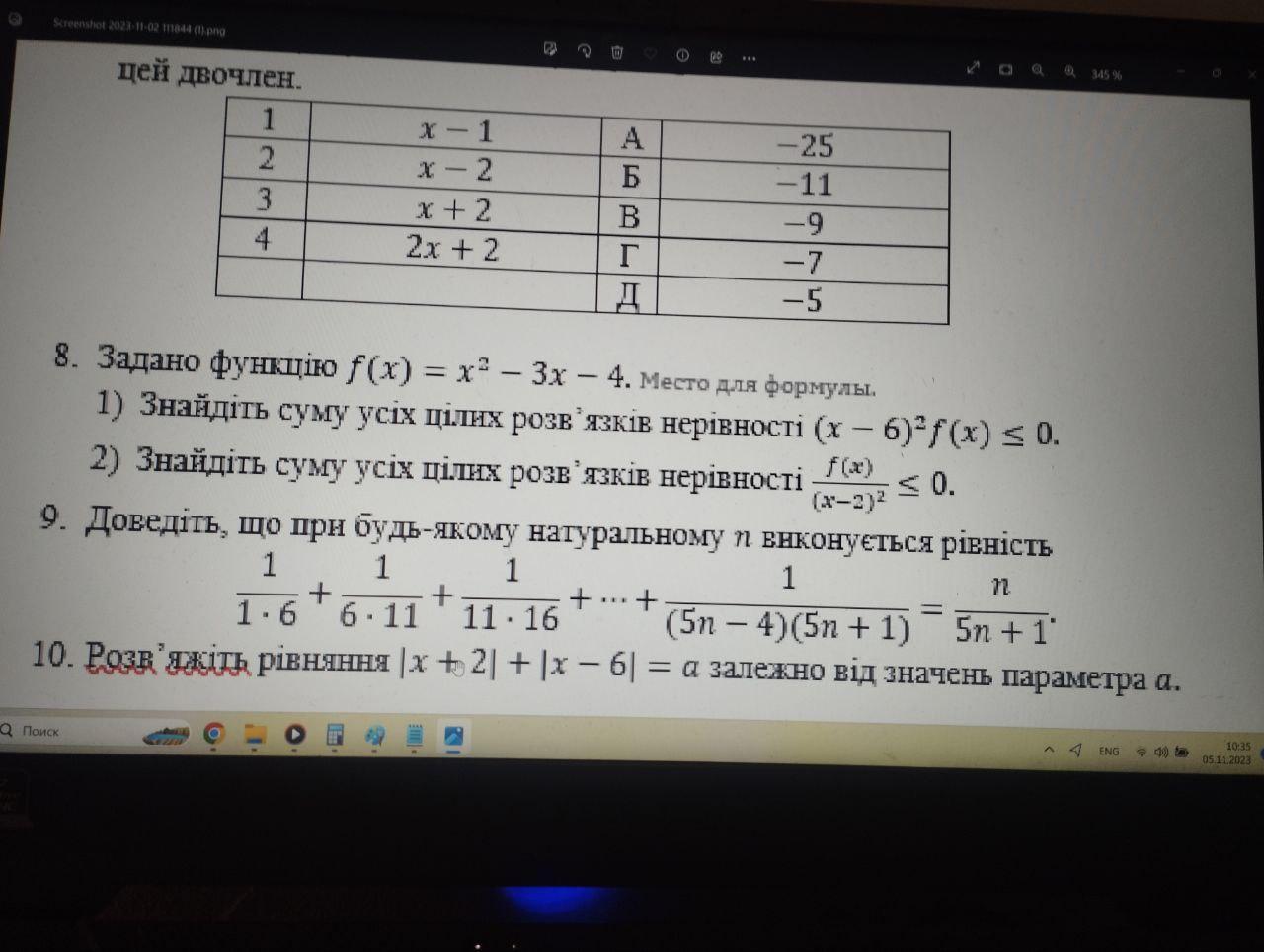
Алгебра, вопрос задал scaromane , 11 месяцев назад

Доведіть, що при будь-якому натуральному п виконується рівність

Приложения:

7x8: Математическая индукция?

Ответы на вопрос

Ответил 7x8

1. Проверяем истинность утверждения для n = 1.

$\frac{1}{1\cdot 6}=\frac{1}{6}$

$\frac{1}{5\cdot 1+1}=\frac{1}{5+1}=\frac{1}{6}$

2. Предполагаем, что истинно для n = k (k -

произвольное натуральное число).

$\frac{1}{1\cdot 6}+\frac{1}{6\cdot 11}+\frac{1}{11\cdot 16}+...+\frac{1}{(5k-4)(5k+1)}=\frac{k}{5k+1}$

3. Доказываем, что истинно, для n = k + 1.

$\frac{1}{1\cdot 6}+\frac{1}{6\cdot 11}+\frac{1}{11\cdot 16}+...+\frac{1}{(5(k+1)-4)(5(k+1)+1)}=\frac{k+1}{5(k+1)+1}$

$\frac{1}{1\cdot 6}+\frac{1}{6\cdot 11}+\frac{1}{11\cdot 16}+...+\frac{1}{(5(k+1)-4)(5(k+1)+1)}=$

$\frac{1}{1\cdot 6}+\frac{1}{6\cdot 11}+\frac{1}{11\cdot 16}+...+\frac{1}{(5k-4)(5k+1)}+\frac{1}{(5(k+1)-4)(5(k+1)+1)}=$

$\frac{k}{5k+1}+\frac{1}{(5(k+1)-4)(5(k+1)+1)}=\frac{k}{5k+1}+\frac{1}{(5k+5-4)(5k+5+1)}=$

$\frac{k}{5k+1}+\frac{1}{(5k+1)(5k+6)}=\frac{k(5k+6)}{(5k+1)(5k+6)}+\frac{1}{(5k+1)(5k+6)}=$

$\frac{k(5k+6)+1}{(5k+1)(5k+6)}=\frac{5k^2+6k+1}{(5k+1)(5k+6)}=\frac{5k^2+5k+k+1}{(5k+1)(5k+6)}=$

$\frac{5k(k+1)+(k+1)}{(5k+1)(5k+6)}=\frac{(k+1)(5k+1)}{(5k+1)(5k+6)}=\frac{k+1}{5k+6}=$

$\frac{k+1}{(5k+5+1}=\frac{k+1}{5(k+1)+1}$

Новые вопросы

Английский язык, 11 месяцев назад

Английский язык, 11 месяцев назад

Українська мова, 11 месяцев назад

Английский язык, 11 месяцев назад

Алгебра, 6 лет назад

Математика, 6 лет назад