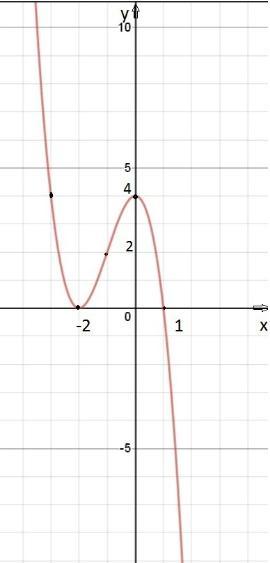
Дослідити функцію в побудувати її графік
х^3-3х^2+4
Ответы на вопрос
Ответ:
Пошаговое объяснение:
1) Область определения:
D(y)=(-∞;+∞);
2) Находим производную функции
y`=(-x³-3x²+4)`=(-x³)`+(-3x²)`+(4)`=-3x²-6x;
3) Находим точки возможных экстремумов, т.е точки, в которых производная равна 0.
у`=0
-3x²-6x=0;
-3x(x+2)=0;
x=0 или х= - 2
4) Применяем достаточное условие экстремума, находим знаки производной слева и справа от этих точек:
____-___(-2)___+___(0)___-___
х=-2 - точка минимума, так как при переходе через точку производная меняет знак с - на +.
х=0- точка максимума, так как при переходе через точку производная меняет знак с + на -.
у(-2)=-(-2)³-3·(-2)²+4=-(-8)-3·4+4=8-12+4=0
у(0)=0³-3·0²+4=4
(-2;0)- точка локального минимума
(0;4)- точка локального максимума
4) Нули функции:
точки пересечения с осью ох.
у=0
-х³-3х²+4=0;
-х³+1-3х²+3=0;
-(х³-1)-3(х²-1)=0
(х-1)(-х²-х-1-3)=0
х-1=0 или -х²-х-4=0
x=1 х²+х+4=0
D=1-16<0 уравнение не имеет корней
(1;0)- точка пересечения с осью ох.
5) Точка пересечения с осью оу (0;4)
6) Дополнительные точки
х=2 у=-2²-3·2²+4=-16
х=-1 у=-(-1)³-3·(-1)²+4=2
х=-3 у=-(-3)³-3·(-3)²+4=27-27+4=4