допоможіть
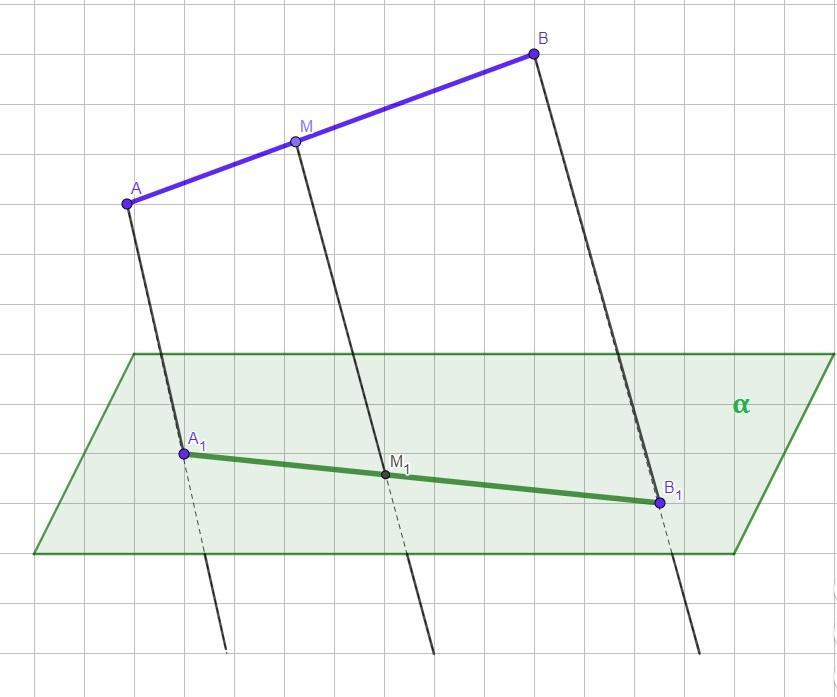
Вiдрiзок прямої АВ поділено точкою М так, що AM : MB - 1:2. Точки А¹, В¹,М¹, - проек тачок А, В, М, вiдповiдно на площину альфа. Знайдіть М¹В¹, якщо А¹В¹ = 15 см.

Ответ:

М₁В₁=10 (см)

Объяснение:

Вiдрiзок прямої АВ поділено точкою М так, що AM : MB - 1:2. Точки А₁, В₁,М₁, - проекції точок А, В, М, вiдповiдно на площину α. Знайдіть М₁В₁, якщо А₁В₁ = 15 см.

Відомо, що при паралельному проектуванні паралельною проекцією відрізка є відрізок.

Тому, так як точки A,M i B - лежать на одній прямій, то A₁, M₁, i B₁  - лежать на одній прямій.

• Відношення паралельних проекцій відрізків, які лежать на одній прямій, дорівнює відношенню самих відрізків:

За умовою AM : MB - 1:2, тому:

Нехай А₁М₁=х (см), а М₁В₁=2х (см), тоді А₁В₁=А₁М₁+М₁В₁=х+2х=3х (см).

А₁В₁ = 15 см, тому складаємо рівняння:

3х=15, х=5 (см)

Отже, М₁В₁=2х=2·5=10 (см)

ВІдповідь: М₁В₁=10 (см)

#SPJ1