Алгебра, вопрос задал lisabonbos , 11 месяцев назад

Допоможіть плізз даю 100 балів
Визначте найбільше ціле відʼємне значення параметра а, за якого рівняння ((a-2)x^2+6x)^2 - 4((a-2) x^2+6x) + 4-а^2= 0 має рівно два корені.

Приложения:

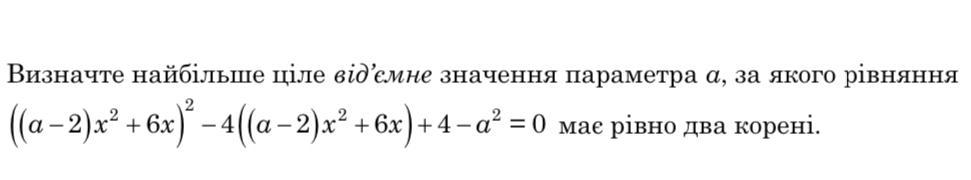
Ответы на вопрос

Ответил 7x8

Ответ:

найбільше ціле відʼємне значення параметра а, за якого рівняння має рівно два корені: $-2$

Объяснение:

$((a-2)x^2+6x)^2 - 4((a-2) x^2+6x) + 4-a^2= 0$

$((a - 2)x^2 + 6x + a - 2)((a - 2)x^2 + 6x - a - 2)=0$

---------------------------------

$a=2$

$(6x)^2 - 4\cdot 6x= 0\\\\36x^2-24x=0\ \ \ |:36\\\\x^2-\frac{2}{3}x=0\\\\x(x-\frac{2}{3})=0\\\\x=0\ \ \ \ \ \ \ x=\frac{2}{3}$

Рівняння має два корені.

$a \neq 2$

---------------------------------

$(a - 2)x^2 + 6x + a - 2=(a - 2)x^2 + 6x - a - 2=0\\\\(a - 2)x^2 + 6x + a - 2=(a - 2)x^2 + 6x - a - 2\\\\a-2=-a-2\\\\a+a=-2+2\\\\2a=0\ \ \ \ |:2\\\\\underline{a=0}$

Рівняння має два корені.

---------------------------------

$((a - 2)x^2 + 6x + a - 2)=0$ - має один корінь

$((a - 2)x^2 + 6x - a - 2)=0$ - має один корінь

$D_1=6^2-4(a-2)(a-2)=36-4(a^2-4a+4)=\\\\ 36-4a^2+16a-16=-4a^2+16a+20\\\\-4a^2+16a+20=0\ \ \ \ |:(-4)\\\\a^2-4a-5=0\\\\a^2-5a+a-5=0\\\\a(a-5)+(a-5)=0\\\\(a-5)(a+1)=0\\\\a-5=0\ \ \ \ \ \ \ \ \ \ a+1=0\\\\a=5\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ a=-1\\\\a\in \left\{-1;5\right\}$

$D_2=0\\\\D_2=6^2-4(a-2)(-a-2)=36+4(a-2)(a+2)=36-4(a^2-4)=\\\\ 36-a^2+16=4a^2+20\\\\4a^2+20=0\\\\4a^2=-20\\\\a\in \emptyset$

$\underline{a\in \emptyset}$

---------------------------------

$(a - 2)x^2 + 6x + a - 2=0$ - має два корені

$(a - 2)x^2 + 6x - a - 2=0$ - не має коренів

$D_1 > 0\\\\-4a^2+16a+20 > 0\ \ \ \ |:(-4)\\\\a^2-4a-5 < 0\\\\a^2-5a+a-5 < 0\\\\a(a-5)+(a-5) < 0\\\\(a-5)(a+1) < 0\\\\a\in (-1;5)$

$D_2 < 0\\\\D_2=4a^2+20\\\\4a^2+20 < 0\\\\4a^2 < -20\\\\a\in \emptyset$

$\underline{a\in \emptyset}$

---------------------------------

$(a - 2)x^2 + 6x + a - 2=0$ - не має коренів

$(a - 2)x^2 + 6x - a - 2=0$ - має два корені

$D_1 < 0\\\\-4a^2+16a+20 < 0\ \ \ \ |:(-4)\\\\a^2-4a-5 > 0\\\\a^2-5a+a-5 > 0\\\\a(a-5)+(a-5) > 0\\\\(a-5)(a+1) > 0\\\\a\in (-\infty;-1)\cup(5;+\infty)$