ДОПОМОЖІТЬ БУДЬ ЛАСКА
Знайти область визначення функції:
Приложения:
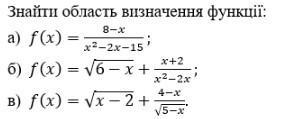
Ответы на вопрос
Ответил pushpull
1
Ответ:
в объяснении
Объяснение:
а) знаменатель дроби не может быть равен 0
x² -2x -15 ≠ 0
разложим знаменатель на множители
x² -2x -15 = 0
по теореме Виета
х₁ * х₂ = -15
х₁ + х₂ = 2
х₁ = 5; х₂ = -2
тогда получим
(х-5)(х+2) ≠ 0
Тогда область определения
D(f) = {x ∈ R: x ≠5; x ≠ -2}
б)
1) подкоренное выражение должно быть ≥ 0
2) знаменатель не может быть равен 0
D(f) = {x ∈ R: x∈ (-∞; 0) ∪ (0; 2) ∪ (2; 6]}
в)
1. подкоренное выражение должно быть ≥ 0
2. знаменатель не может быть равен 0
D(f) = {x ∈ R: x ∈ [2; 5)}
Новые вопросы
Русский язык,
7 месяцев назад
Химия,
7 месяцев назад
Английский язык,
11 месяцев назад
Русский язык,
11 месяцев назад