Допоможіть будь ласка, з рішенням))
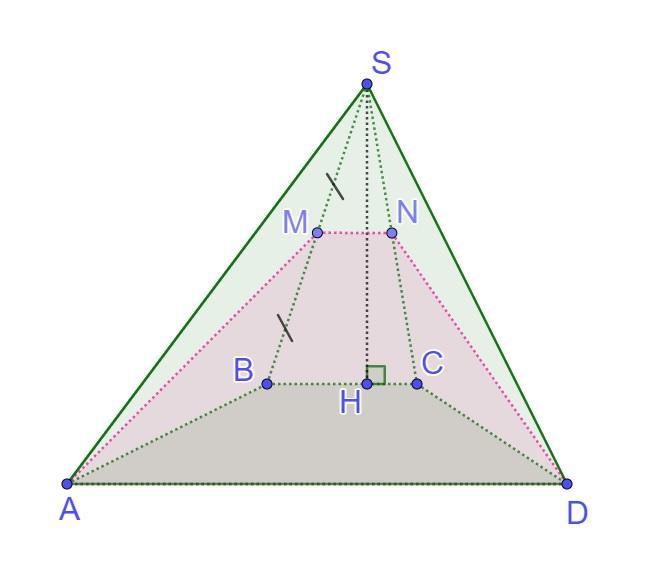
Основою піраміди ЅABCD є трапеція ABCD (BC||AD). Бічна грань SBC, площа якої дорівнює 24,4 см², перпендикулярна до площини основи піраміди. Точка М - середина ребра SB. Площина (MAD) перетинає ребро SC в точці N. Визначте довжину відрізка MN (у см), якщо об'єм піраміди дорівнює 152 см3, а площа її основи - 57 см²

Ответ:

MN = 3,05 см

Объяснение:

Основою піраміди ЅABCD є трапеція ABCD (BC||AD). Бічна грань SBC, площа якої дорівнює 24,4 см², перпендикулярна до площини основи піраміди. Точка М - середина ребра SB. Площина (MAD) перетинає ребро SC в точці N. Визначте довжину відрізка MN (у см), якщо об'єм піраміди дорівнює 152 см³, а площа її основи - 57 см².

За умовою (SBC)⊥(АВС), тому висота SО ∈  (SBC).

AD║BC як основи трапеції. Площина (MAD) проходить через сторону AD трапеції, тоді згідно з теореми, якщо пряма, яка не належить площині, паралельна будь-якій прямій у цій площині, то ця пряма паралельна площині, випливає, що сторона трапеції BC паралельна площині (MAD):

ВС ║ (MAD).

Пряма MN - пряма перетину площини (MAD) і площині (SBC).

Так як  ВС ║ (MAD), вона буде паралельна прямий MN ∈ (MAD), Отже:

MN║BC.

За умовою SM=MB, тобто MN - середня лінія трикутника SBC ⇒ за властивістю середньої лінії трикутника:

MN=1/2·BC.

Знайдемо ВС.

Об'єм піраміди обчислюється за формулою:

де за умовою V = 152 cм³, S = S(ABCD) = 57 cм², Н = SH - висота піраміди.

Звідси:

 (см)

Площа Δ(SBC) обчислюється за формулою:

де за умовою S(SBC) = 24,4 см².

Тоді:

(см)

MN = 1/2 · BC = 6,1 ÷ 2 = 3,05 (см)

Відповідь: 3,05 см